Prove 7.81: Contour Integration for Schaum's Outline Series

[alyafey22]

Here is a problem from Schaum's Outline Series

7.81. Prove that

$$\int^{\infty}_0 \frac{\sin(ax)}{e^{2 \pi x}-1} \,dx = \frac{1}{4} \coth\left( \frac{a}{2} \right) - \frac{1}{2a}$$

I found a solution http://www.mathhelpboards.com/f28/another-integral-5278/#post24397but it is not general , I assumed that $$|a| < 2 \pi $$ but there seemed no restriction in the wording of the problem .

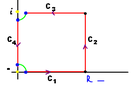
This thread will be dedicated to prove the result using contour integration , any comments or replies are always welcomed .

 

[alyafey22]

I am considering integrating the following function

$$f(z) = \frac{e^{iaz}}{e^{2 \pi z}-1}$$

along one of the contours below

View attachment 951

Hopefully one of the contours will work out .

 

[topsquark]

I am considering integrating the following function

$$f(z) = \frac{e^{iz}}{e^{2 \pi z}-1}$$

along one of the contours below

https://www.physicsforums.com/attachments/951

Hopefully one of the contours will work out .

I am unclear on the second contour. The limits on the integration are on the whole positive real axis. The second contour has no such line segment?

-Dan

 

[Ackbach]

I am considering integrating the following function

$$f(z) = \frac{e^{iz}}{e^{2 \pi z}-1}$$

along one of the contours below

https://www.physicsforums.com/attachments/951

Hopefully one of the contours will work out .

And I think you're going to have problems with the first one as well. Typically, you want to let something get really big. However, the integrand has poles on the imaginary axis every integer multiple of $i$. So you're going to have to find a way to skirt all of those poles. Maybe that's pretty straight-forward, but then again, maybe not.

Or am I misunderstanding your contour? Are you only going to let the real axis part and the corresponding return get big, and not the imaginary axis as well?

 

[alyafey22]

I am unclear on the second contour. The limits on the integration are on the whole positive real axis. The second contour has no such line segment?

-Dan

I made a mistake in the function there is an '' a'' missing it should be

$$f(z) = \frac{e^{i a z}}{e^{2 \pi z}-1}$$

When we integrate the function along the line $$ z = t+i $$ where $$0<t<R$$

$$-\int^R_0 \frac{e^{ia(t+i )}}{e^{2 \pi (t+i)}-1}\, dt = -e^{-a t} \int^R_0 \frac{e^{iat }}{e^{2 \pi t}-1} \, dt$$

very much like the integral we are looking for by taking the imaginary part and $R\to \infty $.

- - - Updated - - -

And I think you're going to have problems with the first one as well. Typically, you want to let something get really big. However, the integrand has poles on the imaginary axis every integer multiple of $i$. So you're going to have to find a way to skirt all of those poles. Maybe that's pretty straight-forward, but then again, maybe not.

Or am I misunderstanding your contour? Are you only going to let the real axis part and the corresponding return get big, and not the imaginary axis as well?

I am only taking $$R \to \infty $$ so the contour will only expand on the x-axis .

 

[Opalg]

I am considering integrating the following function

$$f(z) = \frac{e^{iaz}}{e^{2 \pi z}-1}$$

along one of the contours below

View attachment 953

I thought about using that rectanglar contour, but it seemed too difficult, what with the poles at the corners. However, if you avoid them by going round the little green quadrants as you suggest, everything works out well. Labelling the straight lines in the contour as above, and calling the corresponding integrals $I_1,\ldots,I_4$, what we are looking for is the imaginary part of $I_1$. Note that the real part of $I_1$ diverges as $\varepsilon \to0$, where $\varepsilon$ is the radius of the quadrant. The integral along $C_2$ goes to $0$ as $R\to\infty$, so we can ignore that. The integral $I_3$ will be $-e^{-a}I_1$.

The integrals round the quadrants will be given by the residue theorem. In fact, each of them goes one-quarter clockwise round the pole, so each integral will be $-\frac14$ of $2\pi i$ times the residue. The residues at $0$ and $i$ are $1/(2\pi)$ and $e^{-a}/(2\pi)$, so their combined contribution to the integral is $-\frac i4(1+e^{-a}).$ There are no poles inside the contour, so putting everything together, we see that $$(1-e^{-a})I_1 - \frac i4(1+e^{-a}) + I_4 = 0.$$ That leaves the difficult part, namely $I_4.$ To evaluate that, put $z=iy$ to see that $$I_4 = \int_{1-\varepsilon}^{\varepsilon} \frac{e^{-ay}}{e^{2\pi iy}-1}\,\frac{dy}i = \int_{\varepsilon}^{1-\varepsilon} \frac{e^{-ay}e^{-i\pi y}}{2\sin(\pi y)}\,dy = \int_{\varepsilon}^{1-\varepsilon} \frac{e^{-ay}\bigl(\cos(\pi y) - i\sin(\pi y)\bigr)}{2\sin(\pi y)}\,dy.$$ That looks impossibly complicated. But now remember that we are only interested in the imaginary part of the integral! – which miraculously simplifies (as $\varepsilon\to0$) to $$-\int_0^1 \tfrac12e^{-ay}dy = \frac1{2a}(e^{-a}-1).$$ Therefore $$(1-e^{-a})\int_0^\infty \frac{\sin(ax)}{e^{2 \pi x}-1}\,dx - \frac 14(1+e^{-a}) + \frac1{2a}(e^{-a}-1) = 0,$$ from which $$\int_0^\infty \frac{\sin(ax)}{e^{2 \pi x}-1}\,dx = \frac{1+e^{-a}}{4(1-e^{-a})} + \frac1{2a} = \frac14\coth\Bigl(\frac a2\Bigr) + \frac1{2a}.$$

Somewhere along the line I seem to have mislaid a minus sign, and my solution has the wrong sign for the final term. But I can't see where that happened.

 

[alyafey22]

Hey Oplag , my only difficulty was the integral along the y-axis I didnot think of taking the imaginary part .I thougt I made a mistake somewhere .actually the integral as a whole will diverge only the imaginary part will converge.