Prove Equal Area Triangle & Parallelogram, $\angle ADC=90^{\circ}$

In summary, the conversation discussed the congruence between two triangles using the AAS (angle-angle-side) postulate and the properties of parallel lines and their angles. It was also mentioned that the diagonals of a parallelogram bisect each other and that a parallelogram with equal diagonals is a rectangle. The conversation ended with a question about proving that if two segments are equal, then a certain angle is equal to 90 degrees, and a discussion about the properties of cyclic quadrilaterals.
  • #1
mathlearn
331
0
View attachment 6296

Workings

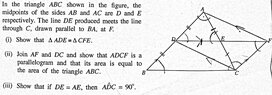
$\triangle ADE \cong \triangle CFE \left(AAS\right)$

$\angle AED = \angle CEF $( vertically opposite angles )
$\angle CFE= \angle EDA $( alternate angles )
$AE=EC $( E midpoint )

$ii.$ADCF is a parallelogram because diagonals bisect each other.

Where is help needed

How should the fact that area of $\triangle ABC$ is equal to parallelogram ADCF be proved ?

Show that if $DE=AE$, then $\angle ADC=90^{\circ}$
 

Attachments

  • New Document 69-Page 1.jpg
    New Document 69-Page 1.jpg
    46.2 KB · Views: 122
Mathematics news on Phys.org
  • #2
What is the area of triangle ADC in relation to the area of triangle ABC?
 
  • #3
greg1313 said:
What is the area of triangle ADC in relation to the area of triangle ABC?

The triangle ADC exactly one half of the area of the triangle ABC

and the parallelogram ADCF is twice the area of triangle ADC and triangle ABC is twice the area of triangle ABC

Now what remains is,

Show that if $DE=AE$, then $\angle ADC=90^{\circ}$

Many THanks :)
 
  • #4
What do the measures of two opposite angles in a cyclic quadrilateral sum to?
 
  • #5
greg1313 said:
What do the measures of two opposite angles in a cyclic quadrilateral sum to?

180 degrees , But a cyclic quadrilateral is not to be seen here (Thinking)
 
  • #6
Look again.
 
  • #7
greg1313 said:
Look again.

:D A little bit confused here,

A cyclic quadrilateral is a quadrilateral whose vertices all touch the circumference of a circle.

But here there is no circle around the figure

Many Thanks :)
 
  • #8
mathlearn said:
Now what remains is,

Show that if $DE=AE$, then $\angle ADC=90^{\circ}$
As an alternative to greg1313's suggestion, what can you say about a parallelogram whose diagonals are equal?
 
  • #9
mathlearn said:
:D A little bit confused here,

A cyclic quadrilateral is a quadrilateral whose vertices all touch the circumference of a circle.

But here there is no circle around the figure

Many Thanks :)

The circle doesn't have to be there. One way of describing a cyclic quadrilateral is "A cyclic quadrilateral is a quadrilateral around which one can draw a circle that touches all four vertices". Now can you make progress with my hint (if you wish to do so)?
 
  • #10
greg1313 said:
The circle doesn't have to be there. One way of describing a cyclic quadrilateral is "A cyclic quadrilateral is a quadrilateral around which one can draw a circle that touches all four vertices". Now can you make progress with my hint (if you wish to do so)?

That's what was exactly missing here,

ADFC is the cyclic quadrilateral and from there

AFD= FDC and ADF= DFC

ADF + FDC=ADC

AFD+DFC=AFC

AFD+DFC+ADF+FDC=180

2ADF + 2FDC = 180

dividing both sides by 2

ADF+FDC=90

ADC=90

Opalg said:
As an alternative to greg1313's suggestion, what can you say about a parallelogram whose diagonals are equal?

Taking it the alternative way,

Both squares and rectangles have their diagonal equal & All angles of them are equal (90°)

It is a rectangle in this case as in a rectangle opposite sides are equal as in a parallelogram

then ADC=90
 

FAQ: Prove Equal Area Triangle & Parallelogram, $\angle ADC=90^{\circ}$

What is the definition of a triangle and parallelogram?

A triangle is a polygon with three edges and three vertices. A parallelogram is a quadrilateral with two pairs of parallel sides.

How do you prove that a triangle and parallelogram have equal area?

To prove that a triangle and parallelogram have equal area, we can use the formula for the area of a triangle (A=1/2*b*h) and the formula for the area of a parallelogram (A=b*h). We can set these two equations equal to each other and solve for h. If the value of h is the same for both equations, then the two shapes have equal area.

What does it mean when $\angle ADC=90^{\circ}$?

When $\angle ADC=90^{\circ}$, it means that angle ADC is a right angle. In other words, it is exactly 90 degrees.

Can a triangle and parallelogram with different side lengths have equal area?

Yes, a triangle and parallelogram with different side lengths can have equal area. As long as the height of the triangle and parallelogram are the same, the two shapes will have equal area.

How is the Pythagorean theorem related to proving equal area between a triangle and parallelogram with $\angle ADC=90^{\circ}$?

The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. In this case, the hypotenuse would be the diagonal of the parallelogram (AD) and the other two sides would be the base (DC) and height (AB) of the triangle. By using the Pythagorean theorem, we can prove that the two shapes have equal area.

Similar threads

MHB Proving Equality of Angles in an Acute Triangle
Replies
4
Views
956
MHB Proof of Parallelogram ABCD: Midpoint X & Y Show Area $\frac{1}{4}$
Replies
5
Views
2K
MHB Can You Find the Angle in This Isosceles Triangle Problem?
Replies
1
Views
1K
MHB Right triangle, feet of altitude, angle bisector and median
Replies
1
Views
1K
MHB Show that AN=1 cm using the knowledge of equiangular triangles.
Replies
9
Views
2K
How does angle of pic provided equal a/2 + 90 degrees?
Replies
5
Views
2K
Proving AD Bisects Angle CAE in Triangle ABC
Replies
3
Views
2K
Does Bisecting Angle A in a 3-4-5 Triangle Divide It into Two Equal Areas?
Replies
1
Views
3K
Prove the angles equal to prove the sides triangle problem
Replies
8
Views
3K

Hot Threads

Recent Insights

Back
Top