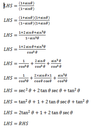The discussion focuses on proving the trigonometric identity (1+sin(x))/(1-sin(x))=2tan^2(x)+1+2tan(x)sec(x). A user seeks assistance in transforming the left-hand side into a non-fractional expression, suggesting the use of the conjugate to simplify the equation. They propose multiplying by (1+sin(x)) to eliminate the denominator. Another participant confirms that this approach is correct and encourages further exploration of the transformation. The conversation emphasizes collaborative problem-solving in trigonometric identities.