Prove inequality of a convex function

[Lambda96]

Homework Statement

Proof that the following inequality holds $\frac{f(x_2)-f(x_1)}{x_2-x_1} \leq \frac{f(x_3)-f(x_1)}{x_3-x_1 } \leq \frac{f(x_3)-f(x_2)}{x_3-x_2}$

Relevant Equations

none

Hi,

I have problem to prove that the following inequality holds

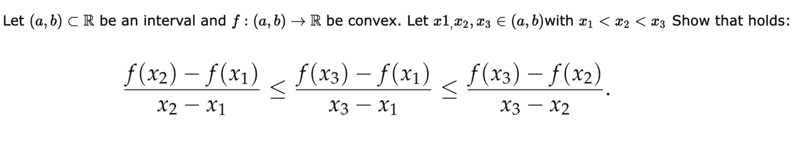
I thought of the following, since it is a convex function and $x_1 < x_2 <x_3$ applies, I started from the following inequality $f(x_2) \leq f(x_3)$ and transformed it further

$$f(x_2) \leq f(x_3)$$
$$f(x_2)-f(x_1) \leq f(x_3)-f(x_1)$$
$$\frac{f(x_2)-f(x_1)}{x_2- x_1} \leq \frac{f(x_3)-f(x_1)}{x_2 - x_1}$$

Since the following applies $x_2 - x_1 \leq x_3 - x_1$ it follows $\frac{f(x_3)-f(x_1)}{x_3- x_1} \leq \frac{f(x_3)-f(x_1)}{x_2 - x_1}$ then follows $\frac{f(x_2)-f(x_1)}{x_2- x_1} \leq \frac{f(x_3)-f(x_1)}{x_3 - x_1}$ i.e. the first part of the inequality

Is my approach correct, or does anyone have a better idea of how I can prove the inequality?

 

[Office_Shredder]

$f(x_2)\leq f(x_3)$ sounds like a condition about increasing functions, not convex functions. What is the definition of a convex function?

Also note your last step is wrong, you basically wrote down $a<b$ and $c< b$ and concluded $a<c$

 

[nuuskur]

$f$ is convex if and only if
$$\frac{f(y)-f(x)}{y-x} \leqslant \frac{f(z)-f(x)}{z-x}$$
for all $a < x < y < z < b$. You have arrived to the right conclusion, but it does not stem from monotonicity ($x^2$ is convex but not monotone, for instance) nor the suspect step in between. Consider instead
$$f(y) \leqslant \frac{z-y}{z-x}f(x)+\frac{y-x}{z-x}f(z).$$

1. Why is this inequality true? (substitute $y=(1-\lambda)x + \lambda z$)
2. Check that it is equivalent to the first inequality.

 

[Lambda96]

Thank you Office_Shredder and nuuskur for your help

Since it is a convex function and $x_2$ lies between $x_1$ and $x_3$, I can represent $x_2$ as follows $x_2=(1- \lambda)x_1 + \lambda x_3$ with $\lambda \in (0,1)$

I then inserted this expression into the first part of the inequality $\frac{f(x_2)-f(x_1)}{x_2-x_1} \leq \frac{f(x_3)-f(x_1)}{x_3-x_1 }$

In order to get the required inequality, I applied the following, since it is a convex function $f((1- \lambda)x_1 + \lambda x_3) \le (1-\lambda)f(x_1) + \lambda f(x_3)$