- #1
anemone
Gold Member
MHB
POTW Director
- 3,883
- 115
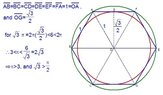
Prove, with no knowledge of the decimal value of $\pi$ should be assumed or used that \(\displaystyle 1\lt \int_{3}^{5} \frac{1}{\sqrt{-x^2+8x-12}}\,dx \lt \frac{2\sqrt{3}}{3}\).