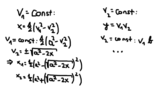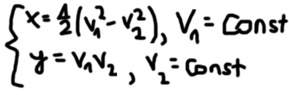berlinvic
- 9
- 0
- Homework Statement
- Prove orthogonality of curves
- Relevant Equations
- Orthogonality condition for curves
I am asked to prove orthogonality of these curves, however my attempts are wrong and there's something I fundamentally misunderstand as I am unable to properly find the graphs (I have only found for a, but I doubt the validity).
Furthermore, I am familiar that to check for othogonality (based on the video ), I need to find both derivatives and make sure their multiplication is equal to -1. However, the introduction of constant a, b in my case doesn't help that at all and I am unable to check for orthogonality.
This has been bugging me for days, I would highly appreciate if someone could put me on the right path to solve this problem
Furthermore, I am familiar that to check for othogonality (based on the video ), I need to find both derivatives and make sure their multiplication is equal to -1. However, the introduction of constant a, b in my case doesn't help that at all and I am unable to check for orthogonality.
This has been bugging me for days, I would highly appreciate if someone could put me on the right path to solve this problem