- #1
Albert1
- 1,221
- 0
View attachment 972
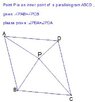
Point P is an iner point of a parallelogram ABCD
given $\angle PAB=\angle PCB$
please prove :$\angle PBA=\angle PDA$
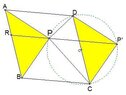
Point P is an iner point of a parallelogram ABCD
given $\angle PAB=\angle PCB$
please prove :$\angle PBA=\angle PDA$