- #1
Albert1
- 1,221
- 0
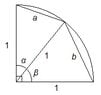
AE is a diameter of a semicicle O,points B,C,D are three points on this semicicle
Given :AB=a ,BC=b ,CD=c ,DE=d ,and AE=2
please prove :
$a^2+b^2+c^2+d^2+abc+bcd < 4$
View attachment 968
Given :AB=a ,BC=b ,CD=c ,DE=d ,and AE=2
please prove :
$a^2+b^2+c^2+d^2+abc+bcd < 4$
View attachment 968
Attachments
Last edited: