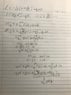- #1
shreddinglicks
- 216
- 6
Member warned that some effort must be shown on homework questions
Homework Statement
Prove Sturm-Liouville differential operator is self adjoint when subjected to Dirichlet, Neumann, or mixed boundary conditions.
Homework Equations
l = -(d/dx)[p(x)(d/dx)] + q(x)
The Attempt at a Solution
I have no idea. If someone can give me a place to start that would be awesome.