Prove that range ##T'## = ##(\text{null}\ T)^0##

[zenterix]

Homework Statement

Prove the following theorem (Axler, Linear Algebra Done Right, Theorem 3.109)

Suppose $V$ and $W$ are finite-dimensional and $T\in L(V,W)$. Then

(a) $\text{dim range}\ T' = \text{dim range}\ T$

(b) $\text{range}\ T'=(\text{null}\ T)^0$

Relevant Equations

(a)

$\text{dim null}\ T' = \text{dim null}\ T + \text{dim}\ W-\text{dim}\ V\tag{1}$

$=\text{dim} W'-\text{dim range}\ T'\tag{2}$

$=\text{dim}\ W-\text{dim range}\ T'\tag{3}$

From (1) and (3) we have

$\text{dim range}\ T'=\text{dim}\ V-\text{dim null}\ T=\text{dim range}\ T\tag{4}$

My question is about item (b).

(b)

Here is what I drew up to try to visualize the result to be proved

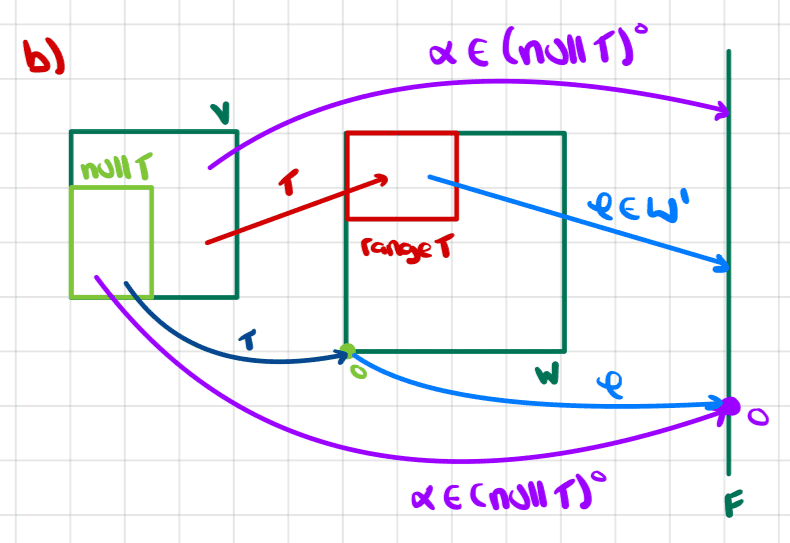
The general idea, I think, is that

1) $(\text{null}\ T)^0$ and $\text{range}\ T'$ are both subspaces of $V'=L(V,\mathbb{F})$.

2) We can show that they have the same dimension.

3)We can show that $\text{range}\ T' \subseteq (\text{null}\ T)^0$

4) From (2) and (3) we can prove that the two subspaces are in fact the same subspace.

Honestly, I did steps (1)-(3) myself and was looking for a way to infer (4) but didn't realize that I could use (2) and (3) to do so, so I looked at the proof in the book.

I'd like to know if there is another way to infer (4).

Here is what I have

$(\text{null}\ T)^0$ is by definition all the linear functionals in $V'$ that map $\text{null}\ T$ to 0 in $\mathbb{F}$.

For every $\varphi\in W'$, the linear functional $\varphi\circ T$ maps $\text{null}\ T$ to 0 in $\mathbb{F}$, so $\varphi\circ T$ is in $(\text{null}\ T)^0$.

Now, at this point, it could be that there are other elements in $(\text{null}\ T)^0$ that are not one of the $\varphi\circ T$.

How can I prove that this is not possible (in an alternative manner to (4))?

 

[zenterix]

I think I found the answer to my question. It uses the dimensions as well.

Let's use a proof by contradiction.

Suppose there were an $\alpha\in (\text{null }\ T)^0$ that is not in $\text{range}\ T'$.

From (a) we know that range $T'$ and range $T$ have the same dimension and so are isomorphic.

In addition, we have dim $V$ = dim null $T$ + dim range $T$.

However, the dimension of the complement of null $T$ in $V$ also has dimension dim range $T$.

Thus this complement is isomorphic with range $T$.

Let $v_1,...,v_n$ be a basis for this complement subspace. $\alpha\in(\text{null}\ T)^0$ maps these to the scalars $f_1, ..., f_n$ in $\mathbb{F}$.

$T$ maps $v_1,...,v_n$ to $w_1, ...,w_n$ in range $T$.

Let's define a $\varphi\in W'$ by $\varphi(w_i)=f_i$ for $i=1,...,n$.

Then, $\varphi\circ T$ maps $v_1,...,v_n$ to $f_1,...,f_n$ and so $\varphi\circ T=\alpha$.

Thus, $\alpha\in \text{range}\ T'$, contradicting our initial assumption.

We can then infer, by proof by contradiction, that all vectors in $(\text{null }\ T)^0$ are in range $T'$.

And since we have proved that range $T'\subseteq (\text{null}\ T)^0$ we can conclude that

$$\text{range}\ T'=(\text{null}\ T)^0$$