Prove that T is a linear transformation

[Hall]

Homework Statement

T is transformation which rotates every vector in 2D by a fixed angle $\phi$. Prove that T is a linear transformation.

Relevant Equations

$T(\mathbf{v_1} + \mathbf{v_2}) = T( \mathbf{v_1}) + T (\mathbf{v_2})$
$T(c\mathbf{v_1}) = c T (\mathbf{v_1})$

We got two vectors $\mathbf{v_1}$ and $\mathbf{v_2}$, their sum is, geometrically, :

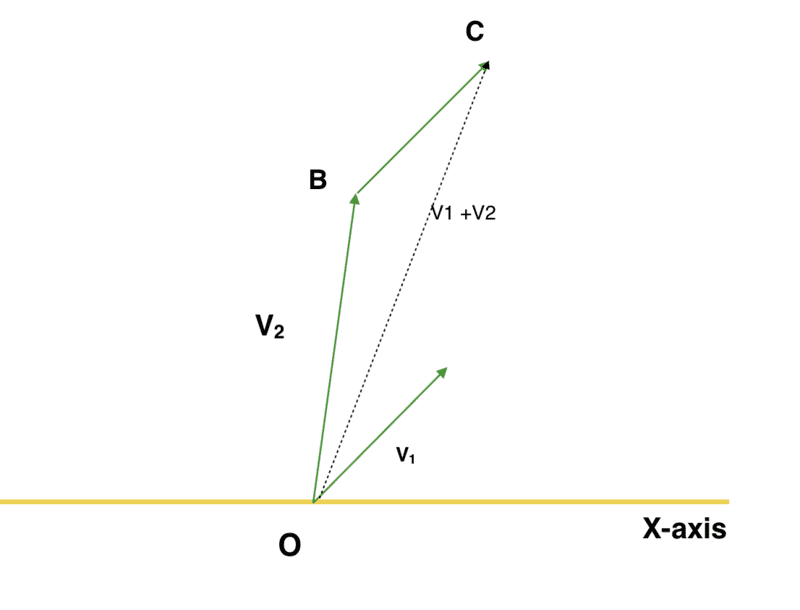
Now, let us rotate the triangle by angle $\phi$ (is this type of things allowed in mathematics?)

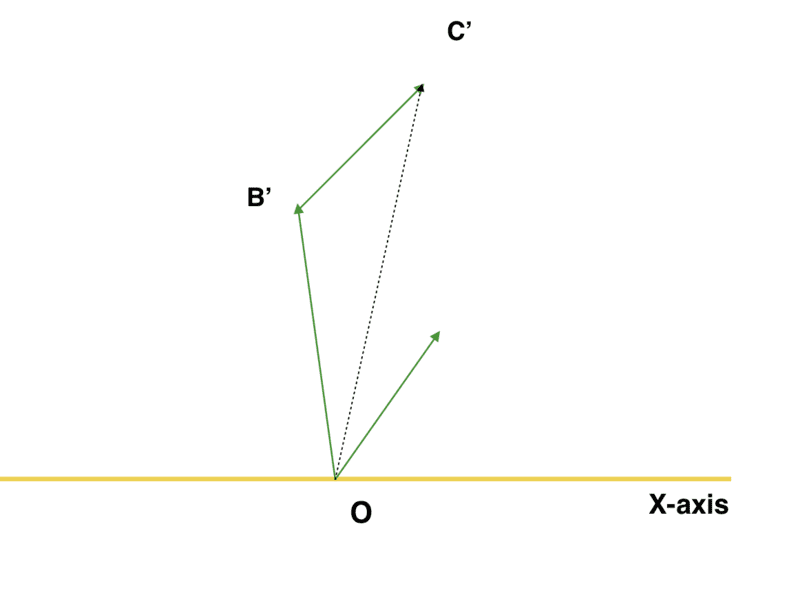
OC got rotated by angle $\phi$, therefore $OC' = T ( \mathbf{v_1} + \mathbf{v_2})$, and similarly $OB' = T(\mathbf{v_2})$. The little pointer guy which is alone, at the right corner (which was marked $\mathbf{v_1}$ in the previous diagram), also got rotated by $\phi$ so, now it represents $T(\mathbf{v_1})$, which gives us $B'C' = T(\mathbf{v_1})$. So, by the geometrical law of vector addition:
$$
\mathbf{OB'} + \mathbf{B'C'} = \mathbf{OC'}$$
$$
T(\mathbf{v_2}) + T(\mathbf{v_2}) = T( \mathbf{v_1 + v_2})$$

AND

$T( c(r \cos \theta, r \sin \theta) ) = (rc \cos (\theta + \phi) , rc \sin (\theta + \phi) )$
$c T (r\cos \theta, r\sin \theta) = c(r \cos (\theta + \phi), r\sin (\theta + \phi) = (rc, \cos (\theta + \phi), rc \sin (\theta + \phi) )= T( c(r \cos \theta, r \sin \theta) )$

We're done, finally.

The big question: Am I right?

 

[Mark44]

For the first part of your proof, dealing with the sum of vectors, I think it would be better to do things algebraically than invoking geometry. Any vector that starts at the origin can be identified by the coordinates of its endpoint.

For the second part, scalar multiples, the following doesn't look right to me. For a given vector that extends from the origin to the point (x, y), in polar form $x = r \cos(\theta)$ and $y = r\sin(\theta)$.
Since the vector doesn't change length in a rotation r doesn't change between the unrotated and rotated versions.

$T( c(x \cos \theta, y \sin \theta) ) = (xc \cos (\theta + \phi) , yc \sin (\theta + \phi) )$
$c T (x\cos \theta, y\sin \theta) = c(x \cos (\theta + \phi), y \sin (\theta + \phi) = (xc, \cos (\theta + \phi), yc \sin (\theta + \phi) )= T( c(x \cos \theta, y \sin \theta) )$

 

[PeroK]

Isn't this why matrices were invented?

 

[Hall]

Isn't this why matrices were invented?

I really don't know.

 

[PeroK]

I really don't know.

Try this:

https://en.wikipedia.org/wiki/Rotation_matrix

 

[Hall]

Try this:

https://en.wikipedia.org/wiki/Rotation_matrix

Now I know.

 

[Hall]

@PeroK
Is T a Linear transformation given that $T(r, \theta)= (r, 2 \theta)$?

I don't think this transformation satisfies the first condition of Linear transformations. Here is the proof:

$\mathbf{v_1}= (r_1, \theta_1)$
$\mathbf{v_2} = (r_2, \theta_2)$
$|\mathbf{v_1} +\mathbf{v_2} |^2 = |\mathbf{v_1}|^2 + |\mathbf{v_2}|^2 - 2|\mathbf{v_1 v_2}| \cos \alpha$

Let's take the transformations now. After applying the transformations, the transformed $\mathbf{v_1}$ and $\mathbf{V_2}$ might not make the same angle (not the angle between them but the one when we placed the tail of v_1 on the head of v_2, however, that also is correct) as before, therefore,
$|T(\mathbf{v_1}) + T(\mathbf{v_2})|^2 = |T(\mathbf{v_1})|^2 + |T(\mathbf{v_2})|^2 - 2 \cos \beta$

But we know that the transformation T is not changing the magnitude of a vector, therefore,
$$
|T(\mathbf{v_1} + \mathbf{v_2} )|^2 =|\mathbf{v_1} +\mathbf{v_2} |^2 = |\mathbf{v_1}|^2 + |\mathbf{v_2}|^2 - 2|\mathbf{v_1 v_2}| \cos \alpha$$
And we have
$$
|T(\mathbf{v_1}) + T (\mathbf{v_2}) |^2 = |\mathbf{v_1}|^2 + |\mathbf{v_2}|^2 - 2|\mathbf{v_1 v_2}| \cos \beta$$

Therefore, $T(\mathbf{v_1} + \mathbf{v_2} ) \neq T(\mathbf{v_1} + T(\mathbf{v_2}$.

But, T does satisfy the second condition:
$$
T ( c (r, \theta)= T (cr, \theta) = (cr, 2 \theta)$$
$$
c T (r, \theta)= c (r, 2\theta)= (cr, 2\theta)$$

So, as everybody else, I conclude that T is not a Linear transformation. But, am I right?

 

[PeroK]

@PeroK
Is T a Linear transformation given that $T(r, \theta)= (r, 2 \theta)$?

Imagine $T$ operating on unit vectors in the $x$ and $y$ directions:
$$T\hat x = \hat x, \ \text{and} \ T\hat y = -\hat x$$ And we see that:
$$T(\hat x + \hat y) = \sqrt 2 \hat y \ne 0 = T \hat x + T\hat y$$

 

[PeroK]

PS you should really be finding specific counterexamples, rather than general formulas that might look different but be equivalent. In any case, finding specific counterexamples is a useful skill, as demonstrated above. I think of it like ju jitsu: finding the weak point and applying a small but potent force where it has the most effect!

 

[Hall]

PS you should really be finding specific counterexamples, rather than general formulas that might look different but be equivalent. In any case, finding specific counterexamples is a useful skill, as demonstrated above. I think of it like ju jitsu: finding the weak point and applying a small but potent force where it has the most effect!

Okay! A nice analogy.

 

[Hall]

@PeroK I got a chick doubt, so I thought a new thread might not be suitable, and it is: Let V be the Linear space of all differentialable functions on (-1,1), and T(f) = x f'(x) [x lies between 1 and -1] Find the rank of T.

I found it easier to subtract the nullity from the dimension of V, but the dimension of V itself is quite hard for me to find. What could be the basis for all differentialable functions on that interval?

 

[PeroK]

I found it easier to subtract the nullity from the dimension of V, but the dimension of V itself is quite hard for me to find. What could be the basis for all differentialable functions on that interval?

It will be infinite dimensional.

 

[Hall]

It will be infinite dimensional.

As I thought. And I thought that we have all the polynomials, trig functions and transcendental functions, which are differetiable in the interval (-1,1); and so it is not possible to construct all of them from some finite basis.

 

[Hall]

It will be infinite dimensional.

Can you please tell me if the space of all convergent sequences whose limit is zero is infinite-dimensional?

 

[PeroK]

Can you please tell me if the space of all convergent sequences whose limit is zero is infinite-dimensional?

Can you prove that?

 

[Hall]

Can you prove that?

No, sorry. I can only imagine that there will be a lot of sequences with different species and their limit being zero, and because of belonging to different species we can not get everyone of them from interbred of few of them.

 

[PeroK]

No, sorry. I can only imagine that there will be a lot of sequences with different species and their limit being zero, and because of belonging to different species we can not get everyone of them from interbred of few of them.

This is linear algebra, not zoology!