Prove that the altitudes of a triangle are concurrent

[Darkmisc]

Homework Statement

Prove that the altitudes of a triangle are concurrent. That is, they meet at a point.

Relevant Equations

Dot product of perpendicular vectors = 0

Hi everyone

I have the solutions to this problem, but I'm not sure I fully understand them.

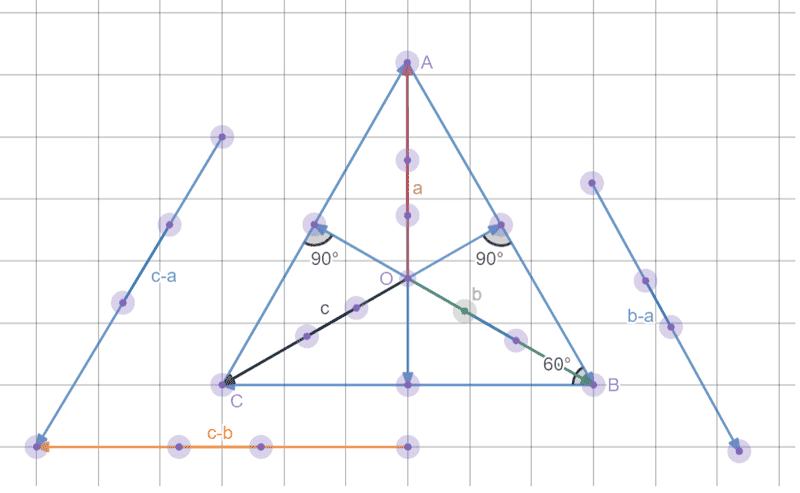
Is the idea behind the proof that all of the following can only be true if the altitudes meet at O?
1. c-b is perpendicular to a
2. c-a is perpendicular to b
3. b-a is perpendicular to c.

That is, if they didn't meet at O, the component vectors of c-b would not cancel so that the resultant vector is perpendicular to a (and the same holds for (c-a)*b and (b-a)*c).Thanks

NB. a = OA, b = OB, c = OC. I used a segment to make labels and I'm stuck with the dots at the end of the segments.

 

[Steve4Physics]

@Lnewqban, I think that the diagram in Post #2 shows the intersection of the bisectors of the three angles (giving the incentre and incircle). But the Post #1 question is about the intersection of the altitudes (at the orthocentre): https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/orthocenter-of-a-triangle-1628503825.png

(It’s worth noting that if one of the triangle’s angles is greater than 90º, then the orthocentre lies outside the triangle. This is never true of the incentre.)

@Darkmisc, your diagram shown in Post #1 uses an equilateral triangle. The question presumably requires consideration of the general case (a scalene triangle). Working with the simplest case of an equilateral triangle could be misleading - probably best avoided!

[Minor edits made.]

 

[Steve4Physics]

Is the idea behind the proof that all of the following can only be true if the altitudes meet at O?
1. c-b is perpendicular to a
2. c-a is perpendicular to b
3. b-a is perpendicular to c.

That is, if they didn't meet at O, the component vectors of c-b would not cancel so that the resultant vector is perpendicular to a (and the same holds for (c-a)*b and (b-a)*c).

Not how I'd explain the process. See if this makes sense...

In the proof, point O is first defined as the point of intersection of just two altitudes: the altitude from A and the altitude from B.

Then a new line is constructed from O to C.

This new line may or may not be the altitude from C. We need to prove that it is indeed the altitude.

To do this we need to show that OC is perpendicular to AB. (Because, by definition, the altitude from C passes through C and is perpendicular to AB.)

This means showing that vector c (corresponding to OC) is perpendicular to vector (b – a) (corroding to AB).

The proof relies on you understanding a couple of key points:

a) how to geometrically subtract one vector from another (that's how we know that the sides of the triangle correspond to (c-a), (c-b) and (b-a)). E.g. see the 2 drawings on the right here: https://www.qsstudy.com/wp-content/uploads/2017/03/Vectors-addition-and-subtraction.jpg

b) the dot product of 2 perpendicular vectors is zero; and conversely, if the dot product of 2 vectors is zero, the vectors must be perpendicular.

Thinking in terms of vector “components” will only confuse the matter.

 

[Lnewqban]

@Lnewqban, I think that the diagram in Post #2 shows the intersection of the bisectors of the three angles (giving the incentre and incircle). But the Post #1 question is about the intersection of the altitudes (at the orthocentre): https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/orthocenter-of-a-triangle-1628503825.png

(It’s worth noting that if one of the triangle’s angles is greater than 90º, then the orthocentre lies outside the triangle. This is never true of the incentre.)

I stand corrected.
Thank you, Steve.
My apologies, @Darkmisc .
Post #2 deleted.