Prove that the field due to a circular arc is same as its bounded tangent at the centre of curvature

[tellmesomething]

Homework Statement

Prove that the field due to a circular arc is same as its bounded tangent at the centre of curvature

Relevant Equations

None

Lambda = charge density

I tried first taking out the field due to the circular arc and I got $$ (lambda / 4π (epsilon knot) ) (2 sin (theta)) $$

For reference this is the arc that was provided in the question of angle 2(theta) and the tangent

What I dont understand is how can the fields be equal as for the arc, the horizontal component of the net electric field is getting cancelled but as for the rod it will not, the centre of curvature that is the point where the e field we have to take out is not at the centre of the rod..

 

[kuruman]

I think you are meant to draw the straight rod tangent to the arc at the arc's midpoint and perpendicular to the bisector of the angle. Then there will be no horizontal field by symmetry.

 

[TSny]

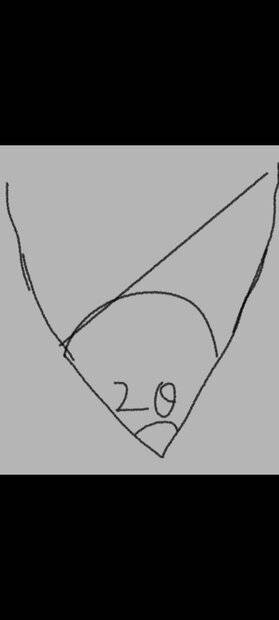
What I dont understand is how can the fields be equal as for the arc, the horizontal component of the net electric field is getting cancelled but as for the rod it will not, the centre of curvature that is the point where the e field we have to take out is not at the centre of the rod..

It's not obvious whether or not the horizontal component of the field at point C will be zero for the charged tangent line.

Do the green element of charge and the red element of charge produce the same field vector at point C?

 

[tellmesomething]

It's not obvious whether or not the horizontal component of the field at point C will be zero for the charged tangent line.
View attachment 345143

Do the green element of charge and the red element of charge produce the same field vector at point C?
View attachment 345145

Actually they do yes I get the same expression for dE for both the circular arc and the tangent

 

[tellmesomething]

I think you are meant to draw the straight rod tangent to the arc at the arc's midpoint and perpendicular to the bisector of the angle. Then there will be no horizontal field by symmetry.

But this is how it was drawn up in the question

 

[kuruman]

But this is how it was drawn up in the question

Sorry, I thought it was your attempt to draw something that was described only with words. Look at the drawing on the right. I augmented @TSny's carefully rendered drawing from post #3 (I hope he doesn't mind) to add features that I can refer to.

I suggest that you find the contributions to the electric field at C from two different sources

1. Element $ds$ (shown in red) on the straight line segment at distance $s$ from point A.
2. Element $Rd\theta$ (shown in green) at angle $\theta$ from radial line CA.

Then find expressions for the horizontal and vertical expressions and do the appropriate integrals which it seems you have done. If anything cancels, it will.

 

[TSny]

Actually they do yes I get the same expression for dE for both the circular arc and the tangent

Good. If you show how you got this result, we can check your work.

Does this essentially solve the problem?

 

[TSny]

I augmented
@TSny's carefully rendered drawing from post #3 (I hope he doesn't mind)

I don’t mind at all.

I suggest that you find the contributions to the electric field at C from two different sources

1. Element $ds$ (shown in red) on the straight line segment at distance $s$ from point A.
2. Element $Rd\theta$ (shown in green) at angle $\theta$ from radial line CA.

Then find expressions for the horizontal and vertical expressions and do the appropriate integrals which it seems you have done. If anything cancels, it will.

After steps 1 and 2 it might not be necessary to consider components or perform any integration.

 

[tellmesomething]

Replying to @TSny and @kuruman

 

[tellmesomething]

I don’t mind at all.


After steps 1 and 2 it might not be necessary to consider components or perform any integration.

But like when integrating we do have to resolve it into its components...is there a way to prove it more rigorously after just proving that the field due to dq charge at angle theta are equal..

 

[tellmesomething]

Replying to @TSny and @kuruman View attachment 345168View attachment 345169

Also the angle theta might not look the same in both the diagrams for clarity I separated it into two diagrams.but they are equal

 

[TSny]

But like when integrating we do have to resolve it into its components...is there a way to prove it more rigorously after just proving that the field due to dq charge at angle theta are equal..

Your work in post #9 looks good.

For each choice of the position of $d \theta$ you have shown that the contribution to the electric field at C is the same for the element of the arc and the corresponding element of the tangent line. The total field at C is just the superposition of the contributions from the various $d \theta$ intervals. Doesn't that prove that the total field at C for the whole arc is the same as for the whole tangent line segment?

 

[tellmesomething]

Your work in post #9 looks good.

For each choice of the position of $d \theta$ you have shown that the contribution to the electric field at C is the same for the element of the arc and the corresponding element of the tangent line. The total field at C is just the superposition of the contributions from the various $d \theta$ intervals. Doesn't that prove that the total field at C for the whole arc is the same as for the whole tangent line segment?

Hmm OK then.. So the field due to the bounded tangent at any orientation will be equal to the field due to the arc at point C?

 

[TSny]

Hmm OK then.. So the field due to the bounded tangent at any orientation will be equal to the field due to the arc at point C?

I'm not sure what you mean by "any orientation". But, the fields of the arc and the bounded tangent would be the same at C for generalizing to the following:

A nice case is a semicircular arc. The "bounded" tangent line is an infinite line:

 

[tellmesomething]

I'm not sure what you mean by "any orientation". But, the fields of the arc and the bounded tangent would be the same at C for generalizing to the following:
View attachment 345171

A nice case is a semicircular arc. The "bounded" tangent line is an infinite line:
View attachment 345173

Exactly but in a video I saw they instead resolved the semi circular arc into two arcs and the tangents to those arcs were two semi infinite rods....I dont know how that follows... Can you explain... For clarity these rods / tangent are perpendicular to the tangent you have drawn in your second diagram...

 

[tellmesomething]

Exactly but in a video I saw they instead resolved the semi circular arc into two arcs and the tangents to those arcs were two semi infinite rods....I dont know how that follows... Can you explain... For clarity these rods / tangent are perpendicular to the tangent you have drawn in your second diagram...

Okay I think I get it the tangent would be parallel to the other boundary since the arcs into which the semi circle has been resolved to would probably be 90°each and any line from the centre to the point of contact of the tangent with the arc is 90 degree. For clarity ive drawn a diagram

 

[TSny]

Is this the scenario?

The field that the arc produces at C would be the same as the field at C due to the two semi-infinte lines.

 

[tellmesomething]

Is this the scenario?
View attachment 345181
The field that the arc produces at C would be the same as the field at C due to the two semi-infinte lines.

Yes, and yes I got it! Since they are parallel as shown in post 16, the tangent will not touch the other end and so it goes off till infinity in one direction

 

[tellmesomething]

Thankyou so much @TSny & @kuruman . Ive understood a very important thing today :)

 

[kuruman]

Is this the scenario?
View attachment 345181
The field that the arc produces at C would be the same as the field at C due to the two semi-infinte lines.

Which means that if you rotate the arc by 180° about the line connecting the two tangent points, the field at C would be zero.

 

[kuruman]

Thankyou so much @TSny & @kuruman . Ive understood a very important thing today :)

And I thnk you for bringing this proof here. I had not come across it before and had not given the matter much thought. I too learned something.

 

[tellmesomething]

Which means that if you rotate the arc by 180° about the line connecting the two tangent points, the field at C would be zero.

Is this what you mean?

If so how is the net field at C zero in the second case...?

 

[kuruman]

Is this what you mean?

No. If you flip everything, you end up with what you started except upside down. Leave the semi-infinite lines alone and flip only the semicircle to get a U shape.

 

[tellmesomething]

No. If you flip everything, you end up with what you started except upside down. Leave the semi-infinite lines alone and flip only the semicircle to get a U shape.

Oh this :

Right everything would cancel off so E at c =0