anemone
Gold Member
MHB
POTW Director
- 3,851
- 115
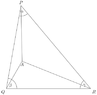
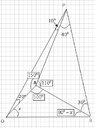
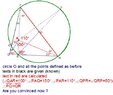
A triangle PQR has the following property:
There is an interior point $A$ such that $\angle APQ=10^{\circ}$, $\angle AQP=20^{\circ}$, $\angle ARP=30^{\circ}$ and $\angle APR=40^{\circ}$.
Prove that the triangle PQR is isosceles.
There is an interior point $A$ such that $\angle APQ=10^{\circ}$, $\angle AQP=20^{\circ}$, $\angle ARP=30^{\circ}$ and $\angle APR=40^{\circ}$.
Prove that the triangle PQR is isosceles.