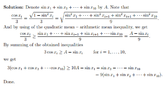lfdahl
Gold Member
MHB
- 747
- 0
If $x_1,x_2,...,x_{10} \in [0;\frac{\pi}{2}]$ and $\sum_{i=1}^{10}\sin^2x_i = 1.$
- then prove, that:
\[ \frac{\sum_{i=1}^{10}\cos x_i}{\sum_{j=1}^{10}\sin x_j} \ge 3\]
- then prove, that:
\[ \frac{\sum_{i=1}^{10}\cos x_i}{\sum_{j=1}^{10}\sin x_j} \ge 3\]