MHB Proving a graph is planar/nonplanar

[Ragnarok7]

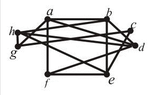
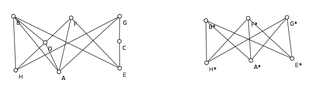
I was given a rather complicated graph as a homework problem, and told to see if it is planar or not. It satisfies the equation $$e\leq 3v-6$$ and has a chromatic number of 4 as well as vertices of degree 5 or below, so there's nothing to rule out planarity there. There are at least 5 vertices of degree 4 or above, and also at least 6 vertices of degree 3 or above, so perhaps it has a subgraph homeomorphic to $$K_{3,3}$$ or $$K_5$$ and so is nonplanar. But I've tried for a long time and I can't get any such subgraph. Is this a trial-and-error process, or is there a better way to go about it?

Thanks!

 

[Ackbach]

Could you please post the graph?

 

[Ragnarok7]

I believe this is reducible to $$K_5$$, but I haven't double-checked it yet.

View attachment 1533

 

[Ackbach]

It's non-coplanar, but it's not isomorphic to either $K_{5}$ or $K_{3,3}$ directly. However, with a few simplifications, you can actually get it down to $K_{3,3}$. I've attached a picture to show you how:

View attachment 1534

So from the left graph, which is isomorphic to the one you were given, perform the following steps (all of which are simplifications; ergo, if the resulting graph is non-coplanar, then the original must have been non-coplanar.)

1. Remove edge BD.
2. Remove edge AD.
3. Consolidate edges HD and DF into one edge HF.
4. Consolidate edges EC and CG into one edge EG.

The result is the graph on the right, which is $K_{3,3}$. Therefore, your graph is non-coplanar.

 

[Ragnarok7]

Thank you so much. It seems easier now that I've had a little more practice, but is it generally just a trial-and-error game?

 

[Ackbach]

Thank you so much. It seems easier now that I've had a little more practice, but is it generally just a trial-and-error game?

For me it was. There might be some nice mathematical trick to doing it in general. I used software: CaRMetal, a sort of open-source version of Geometer's SketchPad. It allows you to move vertices around easily while retaining the connectivity of the original graph.

What happened with me was this: after trying and trying (and failing, oddly enough) to get the graph to be coplanar, I tried to arranged it in a $K_{3,3}$ fashion. I knew $K_{5}$ wasn't going to be present, because there weren't enough vertices with degree 4 to make it isomorphic. So then it was a matter of grouping two sets of vertices to get both sides of $K_{3,3}$, and after some trial and error, I got it, as you can see. Without CaRMetal or some equivalent software, I'd have spent an enormous amount of time on this problem.

 

[Ragnarok7]

Nice! I'll have to check out that software.