Proving a statement about inclusion of subspaces

[JD_PM]

Summary:: I want to understand the following theorem and its proof (which can be found in MSE, link below): Let $V$ be a $n$-dimensional vector space, let $U_i \subseteq V$ be subspaces of $V$ for $i = 1,2,\dots,r$ where $$U_1 \subseteq U_2 \subseteq \dots \subseteq U_r$$
If $r>n+1$ then there exists an $i<r$ for which $U_i = U_{i+1}=\dots=U_r$

I understand that if the subspaces were to be strictly contained (i.e. no possibility of equality between them) then, when going from $U_i$ to $U_{i+1}$, the dimension of the subspace would increase by one. Hence, when reaching $U_r$ the dimension would be greater than $n+1$. However, this is not possible since $U_r$ is a subspace of $V$ and thus has dimension at most $n$.

My issues are

1) I do not see why $\dim U_r>\dim U_i+r-1$ follows from the above argument

2) This is related to 1). I do not see why MSE user egreg here assumes non-equality of the subspaces

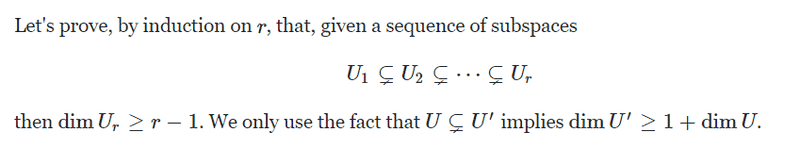
I appreciate your guidance!

 

[PeroK]

Looks like nonsense to me. $U_1 = U_2 = \dots = U_{r-1} = \emptyset$ and $U_r = V$ is a clear counterexample.

In general, the equalities and strict inclusions could be in any order.

 

[fresh_42]

We need some strict inclusions somewhere, e.g. $U_r\subsetneq V.$

The idea is that you cannot build chains that are longer than the finite dimension of $V$. If $U_i\subseteq U_{i+1}$ then they are either equal or $\dim U_{i+1}> \dim U_i$. But we can only use at most $\dim V$ steps. But if everything can be equal, then we could get endless chains with equalities.

One could say: Every chain $U_1\subseteq \ldots \subseteq U_r\subseteq \ldots$ becomes stationary, i.e. there is an index $r$ such that $U_p=U_r$ for all $p>r.$

 

[JD_PM]

The idea is that you cannot build chains that are longer than the finite dimension of $V$. If $U_i\subseteq U_{i+1}$ then they are either equal or $\dim U_{i+1}> \dim U_i$. But we can only use at most $\dim V$ steps. But if everything can be equal, then we could get endless chains with equalities.

Oh, I see. So if we were to deal with strict inclusions, $U_i\subsetneq U_{i+1}$, we would need $\dim U_{i+1}\ge \dim U_i+1$ (i.e. we need to add the +1 difference between dimensions of consecutive strict subspaces).

We need some strict inclusions somewhere, e.g. $U_r\subsetneq V.$

Would you prove it as MSE user egreg or would you approach it differently?

I think I understand his proof but I am really opened to learn other ways.

 

[PeroK]

Oh, I see. So if we were to deal with strict inclusions, $U_i\subsetneq U_{i+1}$, we would need $\dim U_{i+1}\ge \dim U_i+1$ (i.e. we need to add the +1 difference between dimensions of consecutive strict subspaces).
Would you prove it as MSE user egreg or would you approach it differently?

View attachment 286249

I think I understand his proof but I am really opened to learn other ways.

If you think that's a proof, then you have the thorny matter of my counterexample to deal with!

 

[JD_PM]

If you think that's a proof, then you have the thorny matter of my counterexample to deal with!

I am afraid I do not understand your counterexample. Might you please add more details? Thank you.

 

[PeroK]

I am afraid I do not understand your counterexample. Might you please add more details? Thank you.

$V = \mathbb{R^3}, \ U_1 = U_2 = U_3 = \mathbb{R}, U_4 = \mathbb{R^2}, \ U_5 = \mathbb{R^3}$

So: $n = 3, r = 5$ and your proposition fails, as there is no $i < r$ for which $U_i = U_r$.

The "proof" is nonsense, as the proposition is clearly false.

 

[martinbn]

$V = \mathbb{R^3}, \ U_1 = U_2 = U_3 = \mathbb{R}, U_4 = \mathbb{R^2}, \ U_5 = \mathbb{R^3}$

So: $n = 3, r = 5$ and your proposition fails, as there is no $i < r$ for which $U_i = U_r$.

The "proof" is nonsense, as the proposition is clearly false.

$U_1\varsubsetneq U_2$ means that the inclussion is proper, the two spaces cannot be equal.

 

[PeroK]

$U_1\varsubsetneq U_2$ means that the inclussion is proper, the two spaces cannot be equal.

Well, then you cannot have:

If $r>n+1$ then there exists an $i<r$ for which $U_i = U_{i+1}=\dots=U_r$

More to the point, you cannot have more than $n + 1$ subspaces in the first place.

 

[martinbn]

Well, then you cannot have:More to the point, you cannot have more than $n + 1$ subspaces in the first place.

But that's the point, isn't it?

 

[PeroK]

But that's the point, isn't it?

I don't see that as the stated proposition anywhere. The stated proposition is that the subspaces are eventually equal.

 

[martinbn]

I don't see that as the stated proposition anywhere. The stated proposition is that the subspaces are eventually equal.

I read the accual proposition agian, yes, you are right. It is so strange I had missread it.

 

[JD_PM]

$V = \mathbb{R^3}, \ U_1 = U_2 = U_3 = \mathbb{R}, U_4 = \mathbb{R^2}, \ U_5 = \mathbb{R^3}$

So: $n = 3, r = 5$ and your proposition fails, as there is no $i < r$ for which $U_i = U_r$.

The "proof" is nonsense, as the proposition is clearly false.

Ahhh I see the misunderstanding! :) I should have written $U_i = U_{i+1}$ instead of $U_i = U_{i+1}=\dots=U_r$ in the original statement. For the sake of clarity, let me state the theorem again

Let $V$ be a $n$-dimensional vector space, let $U_i \subset V$ be subspaces of $V$ for $i = 1,2,\dots,r$ where $$U_1 \subset U_2 \subset \dots \subset U_r$$
If $r>n+1$ then there exists an $i<r$ for which $U_i = U_{i+1}$

Your counterexample does not apply now as , for instance, we have $U_2 = U_3$.

If you agree, we could proceed to discuss its proof.

 

[PeroK]

Ahhh I see the misunderstanding! :) I should have written $U_i = U_{i+1}$ instead of $U_i = U_{i+1}=\dots=U_r$ in the original statement. For the sake of clarity, let me state the theorem again

Let $V$ be a $n$-dimensional vector space, let $U_i \subset V$ be subspaces of $V$ for $i = 1,2,\dots,r$ where $$U_1 \subset U_2 \subset \dots \subset U_r$$
If $r>n+1$ then there exists an $i<r$ for which $U_i = U_{i+1}$

Your counterexample does not apply now as , for instance, we have $U_2 = U_3$.

If you agree, we could proceed to discuss its proof.

The proof would be simplified, it seems to me, by first showing that $d_1 \le d_2 \dots \le d_r$, where $d_i$ is the dimension of $U_i$.

Then, given that there are only $n+1$ integers from $0$ to $n$ inclusive, if $r > n+1$, then we cannot have strict inequalities all along the line (do you really need to prove this formally?). So, we must have at least one $i < r$, such that $d_i = d_{i+1}$.

Then, show that this implies $U_i = U_{i+1}$.

 

[JD_PM]

The proof would be simplified, it seems to me, by first showing that $d_1 \le d_2 \dots \le d_r$, where $d_i$ is the dimension of $U_i$.

Then, given that there are only $n+1$ integers from $0$ to $n$ inclusive, if $r > n+1$, then we cannot have strict inequalities all along the line (do you really need to prove this formally?). So, we must have at least one $i < r$, such that $d_i = d_{i+1}$.

Then, show that this implies $U_i = U_{i+1}$.

It is not necessary to prove it formally but it might be enlightening to learn it that way so, why not? :)

I'll think more about it and come back.

 

[PeroK]

It is not necessary to prove it formally but it might be enlightening to learn it that way so, why not? :)

I'll think more about it and come back.

If you roll a normal (six-sided) die seven times, can all the outcomes be different? The problem, I find, if you start trying to prove those things is that the things you have to assume to do anything seem no more elementary than the result itself.

Assuming you are not going down into the foundations of mathematics, I think it's safe to assume that you cannot have $r$ distinct numbers in a set of $n+1$ numbers, where $r > n+1$.

If that's not obvious to you, then I don't don't really know how to explain why it's obvious to me!

 

[fresh_42]

I'll think more about it and come back.

To deal with possible strict inclusions, and not strict inclusions is a nightmare as @PeroK's examples show. There are too many possibilities that provide possible counterexamples. Prove my claim in post #3 instead. It is short and clear. Firstly think about which kind of proof looks most promising, and then start from one conclusion to the next, do not jump.

Every chain $U_1\subseteq \ldots \subseteq U_r\subseteq \ldots$ becomes stationary, i.e. there is an index $r$ such that $U_p=U_r$ for all $p>r.$

(https://www.physicsforums.com/insights/how-most-proofs-are-structured-and-how-to-write-them/
is a short essay about proofs in general. Maybe it can help you a bit.)

 

[JD_PM]

I think I understand it!

Please be critic

Every chain $U_1\subseteq \ldots \subseteq U_r\subseteq \ldots$ becomes stationary, i.e. there is an index $r$ such that $U_p=U_r$ for all $p>r.$

What we want to prove: If $r>n+1$ then there exists an $i<r$ for which $U_i = U_{i+1}$.

Approach to prove it: contradiction. We assume that if $r > n+1$ then $\forall i < r$ we have $U_i \neq U_{i + 1}$ (in other words, we assume all inclusions to be strict).

As I was taught during lectures, we define the trivial vectorspace $\{ 0 \}$ to have dimension zero. This implies that $\dim U_1 \geq 0$.

Let us look at $U_1\subsetneq U_2$.

During lectures I learned a theorem stating that given a $n-$dimensional vectorspace $(\Bbb R, V, +)$ and a finite subspace $U$ it holds that $\dim U \leq \dim V$. Hence, taking into account that we deal with strict inclusions, it follows that $\dim U_2 > \dim U_1 \geq 0$. Actually $U_2$ contains (at least) a non-trivial natural number i.e. any $x \in \mathbb{N} \setminus \{ 0\}$. It follows that $\dim U_2 \geq 1$.

It follows that for $U_2\subsetneq U_3$ we get $\dim U_3 \geq 2 = 3 - 1$ and the pattern yields $\dim U_r \geq r - 1$. We are given that $r > n+1$ so it follows that $\dim U_r \geq r - 1 > n + 1 - 1 = n$ i.e. $\dim U_r > n$

"AJÁ", CONTRADICTION! Based on the theorem I stated above, we require the dimension of the vectorspace $V$ and the subspace $U$ to satisfy $\dim U \leq \dim V$

PS: Honestly, this is one of the math problems I've had more fun with in recent times! If you are aware of more problems like this (linear algebra with "dimension analysis" (I am sure there is a better name to be used here but I am a physicist not a mathematician ) involved, please let me know :) ).

 

[fresh_42]

I think I understand it!

Please be critic
What we want to prove: If $r>n+1$ then there exists an $i<r$ for which $U_i = U_{i+1}$.

This is not what I have stated!

Approach to prove it: contradiction. We assume that if $r > n+1$ then $\forall i < r$ we have $U_i \neq U_{i + 1}$ (in other words, we assume all inclusions to be strict).
As I was taught during lectures, we define the trivial vectorspace $\{ 0 \}$ to have dimension zero. This implies that $\dim U_1 \geq 0$.

Let us look at $U_1\subsetneq U_2$.

During lectures I learned a theorem stating that given a $n-$dimensional vectorspace $(\Bbb R, V, +)$ and a finite subspace $U$ it holds that $\dim U \leq \dim V$. Hence, taking into account that we deal with strict inclusions, it follows that $\dim U_2 > \dim U_1 \geq 0$. Actually $U_2$ contains (at least) a non-trivial natural number i.e. any $x \in \mathbb{N} \setminus \{ 0\}$. It follows that $\dim U_2 \geq 1$.

It follows that for $U_2\subsetneq U_3$ we get $\dim U_3 \geq 2 = 3 - 1$ and the pattern yields $\dim U_r \geq r - 1$. We are given that $r > n+1$ so it follows that $\dim U_r \geq r - 1 > n + 1 - 1 = n$ i.e. $\dim U_r > n$

"AJÁ", CONTRADICTION! Based on the theorem I stated above, we require the dimension of the vectorspace $V$ and the subspace $U$ to satisfy $\dim U \leq \dim V$

PS: Honestly, this is one of the math problems I've had more fun with in recent times! If you are aware of more problems like this (linear algebra with "dimension analysis" (I am sure there is a better name to be used here but I am a physicist not a mathematician ) involved, please let me know :) ).

This is correct, except that it is a different statement. You have proven that there cannot be more than $n+1$ strict inclusions in a chain of length $n+1$.

I have claimed, that regardless of how many equalities we have, or do not have, there will be some index form which on there are only equalities left. And note, that I haven't used any dimension in the statement, nor that the chain ends with $V.$

However, you can prove my statement with yours.