Proving an equation in a book about Periodic Structures

[haji-tos]

TL;DR Summary

Proving an equation in a book

Hello everyone,

I am reading some book titled: Periodic Structures: Mode-Matching Approach and Applications in Electromagnetic Engineering.
In Chapter 2, there is an equation as follows:

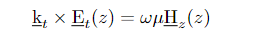where

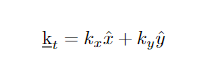. Here the electric field is along the transverse x − y plane like the propagation vector kt.

Now it is said that if we substitute the equation above in the following equation by getting rid of H_z:

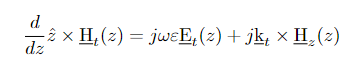
we will obtain the following:

.

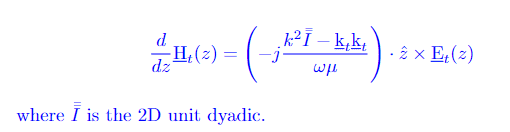When trying to prove this, I don't get the same result. It's been a long time that I am trying to prove this. Can someone please help me prove if this is true ?

Thank you very much.

 

[TSny]

The following two vector identities are very helpful: $$\vec A \times \left( \vec B \times \vec C \right) = \vec B\left(\vec A \cdot \vec C \right) - \vec C\left(\vec A \cdot \vec B \right)$$ $$\vec A \cdot \left( \vec B \times \vec C \right) =\vec B \cdot \left( \vec C \times \vec A \right)$$
Consider the given equation $$\frac d {dz} \hat z \times \vec H_t = j \omega \varepsilon \vec E_t + j \vec k_t \times \vec H_z$$ This can be written as $$ \hat z \times \frac {d \vec H_t} {dz} = j \omega \varepsilon \vec E_t + j \vec k_t \times \vec H_z$$ Apply $\hat z \times$ to both sides: $$ \hat z \times \left(\hat z \times \frac {d \vec H_t} {dz}\right) = j \omega \varepsilon \hat z \times \vec E_t + j \hat z \times \left(\vec k_t \times \vec H_z \right).$$ Use the first vector identity given above to show that this may be reduced to $$\frac {d \vec H_t} {dz}= -j\omega\varepsilon \hat z \times \vec E_t - j \vec k_t \left(\hat z \cdot \vec H_z \right) \,\,\,\,\,\,\,\,\, \rm Eq. 1$$

From the given equation $\vec k_t \times \vec E_t = \omega \mu \vec H_z$ we have $\vec H_z = \frac 1 {\omega \mu} \vec k_t \times \vec E_t$. Substitute this into the last term of Eq. 1 above. Use the second vector identity to finally obtain $$\frac {d \vec H_t} {dz}= -j\omega\varepsilon \hat z \times \vec E_t + \frac j {\omega \mu} \vec k_t \left[\vec k_t \cdot \left( \hat z \times \vec E_t \right) \right]
\,\,\,\,\,\,\,\,\, \rm Eq. 2$$ This can be written in the dyadic form that is given in the first post. You will need to know how $\varepsilon$ is related to $\omega, k$ and $\mu$.

 

[haji-tos]

Hello,

Thank you very much for the help.

I'm struggling to prove another two equations which follows the previous proof.
In the previous post it was proven that

where

The above terms are expressed in terms of the 2D dyadic (2 by 2) matrices.
The eigenvectors and the corresponding eigenvalues for each dyadic are expressed as

Now the two eigenvectors are perpendicular to each other and they are both perpendicular to ẑ. So the three vectors \underline α, \underline β and ẑ form a set of orthonormal basis vectors in a rectangular coordinate system, which are different from the structure coordinate system with x, y and z-axes.
The two dyadics can be expanded then as follows

Up to here all is fine and I've checked it. Now it is said that the 2D dyadic in equations (74) and (75) are expanded in terms of the two orthogonal bases in equations (86) and (87), and that from matrix theory, the transverse vectors in equations (74) and (75) can also be expressed in terms of the superposition of the two bases

where V′(z), V′′(z) are the expanding coefficients for transverse electric field, and I′(z), I′′(z) are those for transverse magnetic field. The above equations are the so-called transmission-line network representation.

Can you please help me prove equations (88) and (89) ? I got stuck here.

Thank you very much !

 

[TSny]

I'm not sure there's much to prove here.

The vectors $\underline \alpha$ and $\underline \beta$ are linearly independent (in fact, orthogonal) and they are both parallel to the x-y plane. So, any vector perpendicular to $\hat z$ can be expanded in terms of $\underline \alpha$ and $\underline \beta$. The left sides of (88) and (89) are vectors that are perpendicular to $\hat z$ and functions of $z$. So, for a given $z$, they can be expressed as shown in (88) and (89) where $V'(z), V''(z), I'(z)$ and $I''(z)$ are the expansion coefficients.

However, if $\underline E_t(z)$ is the transverse electric field then the left side of (88) would be the transverse electric field rotated by 90 degrees around the $\hat z$ axis. So, as I see it, $V'(z)$ and $V''(z)$ are the expansion coefficients for this rotated vector rather than for $\underline E_t(z)$ itself.

 

[haji-tos]

I see, thank you very much for your quick reply.
The thing is that, later on, it is said that for TE mode: V''=0, I''=0 and for the TM mode, V'=0, I'=0. Why is that ?

Thank you again !

 

[TSny]

The thing is that, later on, it is said that for TE mode: V''=0, I''=0 and for the TM mode, V'=0, I'=0. Why is that ?

It's been a while since I've gone through the details of TE and TM waves. But I think the following is true.

TE mode:
The electric field lies in the transverse plane (the plane perpendicular to $\hat z$). So, $\underline E(z) = \underline E_t(z).$

Also, $\underline E_t(z)$ is oriented in the transverse plane such that $\underline E_t(z)$ is perpendicular to $\underline k_t$. Thus, $\underline E_t(z)$ is parallel to $\underline \beta$. This implies $\hat z \times \underline E_t(z)$ is parallel to $\underline \alpha$. So, $V'' = 0$.

$\underline H_t(z)$ is perpendicular to $\underline E_t(z)$, so $\underline H_t(z)$ must also be parallel to $\underline \alpha$. Hence, $I'' = 0$.

TM mode:
The analysis is similar. Then, instead of $\underline E_t(z)$ being parallel to $\underline \beta$, we have $\underline H_t(z)$ parallel to $\underline \beta$. So, $I' = 0$.

$\underline E_t(z)$ is perpendicular to $\underline H_t(z)$ which implies $\underline E_t(z)$ is parallel to $\underline \alpha$. Thus, $\hat z \times \underline E_t(z)$ is parallel to $\underline \beta.$ Therefore, $V' = 0$.

 

[haji-tos]

Great !! Thank you very much for your help ! I really appreciate it