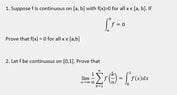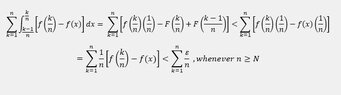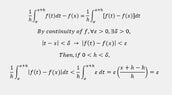joypav
- 149
- 0
Okay, these are my last questions and then I'll get out of your hair for a while.
For 1, I have already done a proof by contradiction, but I'm supposed to also do a direct proof. Seems like it should be simple?
For 2, this seems obvious because it's the definition of an integral. My delta is 1/n. So I should try choosing a smart point, then I need to use an epsilon argument to prove that they are equal?
View attachment 6493
For 1, I have already done a proof by contradiction, but I'm supposed to also do a direct proof. Seems like it should be simple?
For 2, this seems obvious because it's the definition of an integral. My delta is 1/n. So I should try choosing a smart point, then I need to use an epsilon argument to prove that they are equal?
View attachment 6493