- #1
anemone
Gold Member
MHB
POTW Director
- 3,883
- 115
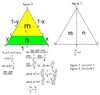
A line divides an equilateral triangle into two parts with the same perimeter and having areas $A_1$ and $A_2$ respectively. Prove that $\dfrac{7}{9} \le \dfrac{A_1}{A_2} \le \dfrac{9}{7}$.