Proving Countability: Positive Rational Numbers & Union of Countable Sets

[mathmari]

Hey!

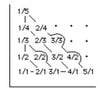
1. Show that the set of all positive rational numbers is a countable set.
   (Hint: Consider all points in the first quadrant of the plane of which the coordinates x and y are integers.)
2. Show that the union of a countable number of countable sets is a countable set.

I have done the following:

1. Let $x,y>0$. We write a positive rational $\frac{x}{y}$ at the point (x, y) in the plane in the first quadrant. Now we have to count these points, or not?
2. Do we have to use induction here?

(Wondering)

 

[I like Serena]

Hey mathmari!

We should make a so called swan walk. That applies to both your problems.
The swan walk for the positive rationals is 1/1, 1/2, 2/1, 3/1, 2/2, 1/3, 1/4, ... (Thinking)

 

[Greg]

As an aside, see Chapter 1, exercise 4 (Examples I) of that PDF. I believe the general result implies countability.

You'll have to scroll down to see exercise 4; the link above is not direct.

 

[mathmari]

We should make a so called swan walk. That applies to both your problems.
The swan walk for the positive rationals is 1/1, 1/2, 2/1, 3/1, 2/2, 1/3, 1/4, ... (Thinking)

Does this mean that we correspond to these rationals the respective point and then we count them as follows?

View attachment 8481

(Wondering)

- - - Updated - - -

As an aside, see Chapter 1, exercise 4 (Examples I) of that PDF. I believe the general result implies countability.

You'll have to scroll down to see exercise 4; the link above is not direct.

So, do we have to write the positive rationals as a sequence? (Wondering)

 

[I like Serena]

Does this mean that we correspond to these rationals the respective point and then we count them as follows?

So, do we have to write the positive rationals as a sequence? (Wondering)

Yes.
greg1313's reference shows a slightly different swan-walk, which boils down to the same thing.
We can write the positive rationals as a sequence, which means that we can 'count' them.
That is, we can define a mapping $\mathbb N \to \mathbb Q_{>0}$ that is surjective, which shows that the positive rationals are countable. (Thinking)

 

[mathmari]

Yes.
greg1313's reference shows a slightly different swan-walk, which boils down to the same thing.
We can write the positive rationals as sequence, which means that we can 'count' them.
That is, we can define a mapping $\mathbb N \to \mathbb Q_{>0}$ that is surjective, which shows that the positive rationals are countable. (Thinking)

Ah ok!

But using the given hint, do we 'count' the positive rationals as in the picture of #4 ? If yes, how could we prove that formally without just with the picture?

(Wondering)

 

[I like Serena]

Ah ok!

But using the given hint, do we 'count' the positive rationals as in the picture of #4 ? If yes, how could we prove that formally without just with the picture?

Any positive rational can be written as $\frac p q$ where $p$ and $q$ are positive integers.
So each positive rational will show up in the sequence.
We might formalize the actual sequence a bit more, defining the actual mapping.
Did you try? Otherwise you can check out greg1313's reference. (Thinking)

 

[mathmari]

Any positive rational can be written as $\frac p q$ where $p$ and $q$ are positive integers.
So each positive rational will show up in the sequence.
We might formalize the actual sequence a bit more, defining the actual mapping.
Did you try?

1/1, 1/2, 2/1, 3/1, 2/2, 1/3, 1/4, ...

First we have all the fractions where the sum of numerator and denominator is equal to 2, then all the fractions where the sum of numerator and denominator is equal to 3, then all the fractions where the sum of numerator and denominator is equal to 4, etc.

The fraction p/q will appear if we write down all the fractions with sum of numerator and denominator equal to $p+q$.

Do we have to justify that we get this fraction after finite number of terms? Is everything correct? Or did you mean something else? (Wondering)

 

[I like Serena]

1/1, 1/2, 2/1, 3/1, 2/2, 1/3, 1/4, ...

First we have all the fractions where the sum of numerator and denominator is equal to 2, then all the fractions where the sum of numerator and denominator is equal to 3, then all the fractions where the sum of numerator and denominator is equal to 4, etc.

The fraction p/q will appear if we write down all the fractions with sum of numerator and denominator equal to $p+q$.

Do we have to justify that we get this fraction after finite number of terms? Is everything correct? Or did you mean something else?

Yes. That is what I meant. And I believe it is sufficient for a proof. (Nod)

 

[mathmari]

Yes. That is what I meant. And I believe it is sufficient for a proof. (Nod)

Ah ok! Great! (Nerd) What about the second question to show that the union of a countable number of countable sets is a countable set?
Do we have to show first that it holds for two sets and then we show the desired by induction?

Let $A=(a_1, a_2, \ldots )$, $B=(b_1, b_2, \ldots )$ be two countable sets. We define $f:\mathbb{N}\times\mathbb{N}\rightarrow A\times B$ with $f(n,m)=(a_n, b_m)$. This map is surjective, isn't it?
We have that $\mathbb{N}\times\mathbb{N}$ is counatble, right? Then it follows that $A\times B$ is also countable.

Is this part correct? (Wondering) Now we have to use the induction to show that $\displaystyle{\bigcup_{n\in \mathbb{N}}M_n}$ is countable:

Base case: For $n=1$ it holds since then we have just one set, which is countable.

Inductive Hypothesis: We suppose that the statement holds for $n=k$.

Inductive step: We want to show that it holds for $n=k+1$. We have that $\bigcup_{n=1}^{k+1}M_n=\bigcup_{n=1}^{k}M_n\cup M_{k+1}$. The first one $\bigcup_{n=1}^{k}M_n$ is countable from the inctuctive hypothesis and $M_{k+1}$ is also ccountable.
So we have a union of two countable sets, which is countable because of the above argument.

Is everything correct? (Wondering)

 

[I like Serena]

Ah ok! Great! (Nerd) What about the second question to show that the union of a countable number of countable sets is a countable set?
Do we have to show first that it holds for two sets and then we show the desired by induction?

Let $A=(a_1, a_2, \ldots )$, $B=(b_1, b_2, \ldots )$ be two countable sets. We define $f:\mathbb{N}\times\mathbb{N}\rightarrow A\times B$ with $f(n,m)=(a_n, b_m)$. This map is surjective, isn't it?
We have that $\mathbb{N}\times\mathbb{N}$ is counatble, right? Then it follows that $A\times B$ is also countable.

Is this part correct?

It is correct, although you may want to explain why $\mathbb{N}\times\mathbb{N}$ is countable.
It is countable for the same reason as $\mathbb Q_{>0}$, which is because we can define a swan walk.
That is, we can define a surjective map $\mathbb N \to \mathbb N \times \mathbb N$, showing that it is countable.

Now we have to use the induction to show that $\displaystyle{\bigcup_{n\in \mathbb{N}}M_n}$ is countable:

Base case: For $n=1$ it holds since then we have just one set, which is countable.

Inductive Hypothesis: We suppose that the statement holds for $n=k$.

Inductive step: We want to show that it holds for $n=k+1$. We have that $\bigcup_{n=1}^{k+1}M_n=\bigcup_{n=1}^{k}M_n\cup M_{k+1}$. The first one $\bigcup_{n=1}^{k}M_n$ is countable from the inctuctive hypothesis and $M_{k+1}$ is also ccountable.
So we have a union of two countable sets, which is countable because of the above argument.

Is everything correct?

I believe so yes.
EDIT: As Country Boy mentions below, induction is not good enough. We really need a surjective mapping of $\mathbb N$ to all elements.
Btw, we're mixing cartesian products and unions, which is strictly speaking not correct.Instead we can also define a swan walk through all the sets.
Let $a_{ij}$ be the $j$th element of the $i$th set.
Then $a_{11}, a_{12}, a_{21}, a_{13}, a_{22}, ...$ is a countable sequence that contains all elements in all sets. (Nerd)

 

[HOI]

Ah ok! Great! (Nerd) What about the second question to show that the union of a countable number of countable sets is a countable set?
Do we have to show first that it holds for two sets and then we show the desired by induction?

NO! "Induction" would show only that the union of any finite number of countable sets is countable.

Let $A=(a_1, a_2, \ldots )$, $B=(b_1, b_2, \ldots )$ be two countable sets. We define $f:\mathbb{N}\times\mathbb{N}\rightarrow A\times B$ with $f(n,m)=(a_n, b_m)$. This map is surjective, isn't it?
We have that $\mathbb{N}\times\mathbb{N}$ is counatble, right? Then it follows that $A\times B$ is also countable.

Is this part correct? (Wondering) Now we have to use the induction to show that $\displaystyle{\bigcup_{n\in \mathbb{N}}M_n}$ is countable:

Base case: For $n=1$ it holds since then we have just one set, which is countable.

Inductive Hypothesis: We suppose that the statement holds for $n=k$.

Inductive step: We want to show that it holds for $n=k+1$. We have that $\bigcup_{n=1}^{k+1}M_n=\bigcup_{n=1}^{k}M_n\cup M_{k+1}$. The first one $\bigcup_{n=1}^{k}M_n$ is countable from the inctuctive hypothesis and $M_{k+1}$ is also ccountable.
So we have a union of two countable sets, which is countable because of the above argument.

Is everything correct? (Wondering)