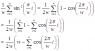- #1
Proving Discrete Sum Equation - Step-by-Step Guide and Tips
In summary, the conversation is about proving an equation and using a double angle formula to express sin(x)^2 in terms of cos(2x). The last term in the expression (sum(cos(2pi*i/w))) is equal to 0 due to Euler's formula, e^(ix)=cos(x)+i*sin(x). This allows one to treat the sum of the cos term as the real part of the sum of a geometric series. It is not an assumption, as the term is exceedingly small and can be proven to be equal to 0.
- #2
Dick
Science Advisor
Homework Helper
- 26,258
- 623
Start by using a double angle formula to express sin(x)^2 in terms of cos(2x). Now get started.
- #3
- #4
darkfeffy
- 17
- 0
Thinking it might just be an assumption that this last term is exceedingly small compared to the first.
- #5
Dick
Science Advisor
Homework Helper
- 26,258
- 623
darkfeffy said:
Do you know Euler's formula, e^(ix)=cos(x)+i*sin(x) (i the imaginary unit, not the integer index)? That would let you treat the sum of the cos term as the real part of the sum of a geometric series. And no, there's no approximation here. The cos part really does sum to zero.
Last edited:
- #6
- 15,464
- 690
You are correct in that the term is exceedingly small (zero is an exceedingly small number). You are incorrect in that is an assumption.darkfeffy said:
- #7
darkfeffy
- 17
- 0
Thanks Dick.Dick said:
- #8
darkfeffy
- 17
- 0
Thanks DH for your brilliant reply which really doesn't add much information :-)D H said:
FAQ: Proving Discrete Sum Equation - Step-by-Step Guide and Tips
What is a discrete sum?
A discrete sum is a mathematical operation that involves adding a finite number of terms together. It is also known as a finite sum or a summation. Each term in a discrete sum is represented by a variable or a constant, and the sum is denoted by the symbol ∑ (sigma).
What is the purpose of proving a discrete sum?
The purpose of proving a discrete sum is to verify the accuracy and validity of the sum. This is important in mathematics and scientific research, as it allows for the verification of calculations and the confirmation of results.
How do you prove a discrete sum?
To prove a discrete sum, you must first write out the full expression of the sum, including all the terms and the limits of the summation. Then, you can use mathematical properties and techniques, such as the distributive property, to simplify the expression and arrive at a known result or a desired solution.
What are some common methods used to prove a discrete sum?
Some common methods used to prove a discrete sum include mathematical induction, telescoping sums, and the use of summation formulas. These methods rely on algebraic manipulation and pattern recognition to simplify the expression and prove the sum.
Why is it important to understand how to prove a discrete sum?
Understanding how to prove a discrete sum is important for various reasons. It allows for the verification of calculations and the confirmation of results in mathematics and scientific research. It also helps in the development of problem-solving skills and the ability to recognize patterns and apply mathematical concepts.