Proving inverse of a 2 x 2 matrix is really an inverse

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this,

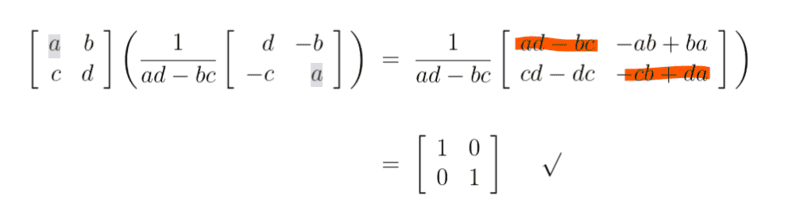
Dose someone please know how $ad - bc$ and $-cb + da$ are equal to 1?

Many thanks!

 

[FactChecker]

They are not equal to 1. They are both divided by ad-bc, which gives 1.

 

[member 731016]

They are not equal to 1. They are both divided by ad-bc, which gives 1.

Oh thank you @FactChecker ! I see now

 

[fresh_42]

This formula
$$
\begin{pmatrix}a&b\\c&d\end{pmatrix}^{-1}=\begin{pmatrix}d&-b\\-c&a\end{pmatrix} \cdot (ad-bc)^{-1}
$$

is so easy to memorize ...

1. swap the diagonal entries $a \leftrightarrow d$
2. put a minus sign in front of the entries on the side diagonal $b \rightarrow -b\, , \,c\rightarrow -c$
3. and finally, divide by the determinant $ad-bc.$

... that I use it whenever I have to solve a linear equation system in $2$ variables.

E.g. I wanted to write $16 \cdot 24$ and $8\cdot 48$ as $(n-m)\cdot (n+m)$ today. That goes:
\begin{align*}
\begin{pmatrix}1&-1\\1&1 \end{pmatrix}\cdot \begin{pmatrix}n\\m\end{pmatrix}=\begin{pmatrix}16\\24 \end{pmatrix}
\end{align*}
Then by doing the procedure as described I get
\begin{align*}
\begin{pmatrix}n\\m \end{pmatrix}=\begin{pmatrix}1&1\\-1&1 \end{pmatrix}\cdot \begin{pmatrix}16\\24 \end{pmatrix}\cdot \underbrace{(1\cdot 1- (-1\cdot 1))^{-1}}_{=1/2}=\begin{pmatrix}1&1\\-1&1 \end{pmatrix}\cdot \begin{pmatrix}8\\12 \end{pmatrix}=\begin{pmatrix}8+12\\ -8+12\end{pmatrix}=\begin{pmatrix}20\\4 \end{pmatrix}
\end{align*}
Same with the other product $8\cdot 48.$

I know this was an easy example and could probably just "be seen". But I'm better with algorithms than "seeing" things. Once you get used to that procedure it is really easy to follow. Especially if the examples are a bit more complicated.