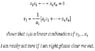Proving Linear Dependence in a Set of Vectors

[ahamdiheme]

Homework Statement

Suppose v_1,...,v_k is a linearly dependent set. Then show that one of the vectors must be a linear combination of the others.

Homework Equations

.

The Attempt at a Solution

I have attached an attempt at the problem. Thank you for help

 

[HallsofIvy]

Your solution says a_1v_1+ a_2v_2+ a_3v_3+ \cdot\cdot\cdot+ a_nv_n= 0 and then you go to v_1= (-1/a_1)(a_2v_2+ a_3v_3+ \cdot\cdot\cdot+ a_nv_n)

That's pretty good. The only problem is you don't know that a₁ is not 0! If it is you can't solve for v₁. What you DO know, from the definition of "dependent", that you didn't say is that at least one of the "a_i" is NOT 0. You don't know which one but you can always say "Let "k" be such that a_k is not 0". Then what?

 

[ahamdiheme]

Thank you. What if i say let k:a_k not equal to 0
and v₁ is a linear combination of v₂,...,v_n iff a₁=a_k

 

[Mark44]

You want to show that v_k is a linear combination of the rest of the vectors. IOW, that v_k is a linear combination of v₁, v₂, ..., v_k-1, v_k+1, ..., v_n.

 

[ahamdiheme]

ok, i think i get it