pholee95
- 9
- 0
I don't know how to start proving this theorem, so can someone please help? I need to prove that the circumcircles all intersect at a point M. Thank you!
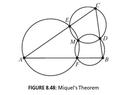
Miquel's Theorem: If triangleABC is any triangle, and points D, E, F are chosen in the interiors of the sides BC, AC, and AB, respectively, then the circumcircles for triangleAEF, triangleBDF, and triangleCDE intersect in a point M.
I have attached here the figure of theorem.
Miquel's Theorem: If triangleABC is any triangle, and points D, E, F are chosen in the interiors of the sides BC, AC, and AB, respectively, then the circumcircles for triangleAEF, triangleBDF, and triangleCDE intersect in a point M.
I have attached here the figure of theorem.