Albert1
- 1,221
- 0
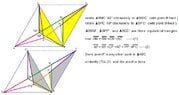
M is an inner point of acute $\triangle ABC$
$\angle AMB=\angle BMC=\angle CMA=120^ o$
point P is another point in $\triangle ABC$
Prove :$PA+PB+PC\geq MA+MB+MC$
$\angle AMB=\angle BMC=\angle CMA=120^ o$
point P is another point in $\triangle ABC$
Prove :$PA+PB+PC\geq MA+MB+MC$