Proving Perpendicularity of DB.AC in a Tetrahedron

[Procrastinate]

Could someone please give me a hint on this question?

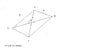
In the tetrahedron ABCD, AB is perpendicular to DC and AD is perpendicular to BC, prove that DB is perpendicular to AC.

This is what I am stuck on:

DB.AC = (DC+CB).(AD+dc)
=DC.AD +DC.DC+CB.AD+CB.DC
=(CA+AD).AD+d.d+(CA+AB).DC
=CA.AD+AD.AD+d.d+CA.DC+ab.dc
=-c.d+d.d+d.d+-c.(CA+AD)
-c.d+d.d+d.d+c.c+-c.d
=2d.d+c.c-2(c.d)

See attachment.

 

[foxjwill]

Are you sure you wrote down the question correctly? As it stands, I don't think any tetrahedron's going to satisfy your givens. It seems to me that both AB and BC would have to be perpendicular to the plane through ABC; but then AB and BC would parallel, contradicting the fact that they intersect. However, it's 3:45am by me, so I might have missed something.

 

[ehild]

The problem is OK.
If you project the vertex A onto the plane BCD the projected edges of the tetrahedron are also perpendicular. This might help...

ehild