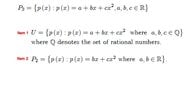Proving Subspace Properties for Sets of Polynomials in P3

[chukkitty]

Hello,

I want ask some subspace problems. Attachment is a question.
contains all polynomials with degree less than 3 and with real coefficients.

I want prove that item 1 and item 2 are subspace or not.

Am I insert real number to the item 1& 2 equation to test as follows:
(a) 0 ∈ S.
(b) S is closed under vector addition.
(c) S is closed under scalar multiplication.

Would you mind tell me how Determine whether the following sets are subspaces of P3. If it is a subspace, prove it. If it is not a subspace, give a counter-example.

Best Regard
Kitty

 

[ModusPonens]

Indeed what you have to do is to provide a proof that the sets have the 0, are closed to addition and scalar multiplication.

The important thing, that works for all problems of this type is that, when you have a set $\{ x: C(x) \}$, where $C(x)$ is the condition for the x to belong to the set, to verify that:

1-C(0) is true. This implies that 0 is in the set;
2-If C(x) and C(y) is true (equivalently, if x and y are in the set), then C(x+y) is true. This implies that x+y is in the set;
3- If C(x) is true, then $C(ax)$ is true, where $a$ is a scalar. This implies that $ax$ is in the set.The condition C for the first set in your exercise is a condition on a polinomial p. $C(p)$ is $p=a+bx+cx^2 \wedge a,b,c\in \mathbb{Q}$.

Teach a man how to fish... ;)

 

[alyafey22]

(a) 0 ∈ S.
(b) S is closed under vector addition.
(c) S is closed under scalar multiplication.

In general the first is not needed since it is already covered in the third condition . Since the set of rational numbers is closed under addition and multiplications , item 1 forms a subspace .

For item 2 , I think there is a mistake since you are not specifying what is c ?

 

[ModusPonens]

In general the first is not needed since it is already covered in the third condition . Since the set of rational numbers is closed under addition and multiplications , item 1 forms a subspace .

For item 2 , I think there is a mistake since you are not specifying what is c ?

I think item 1 is not a subspace because it is not closed by multiplication by real scalars.

 

[alyafey22]

I think item 1 is not a subspace because it is not closed by multiplication by real scalars.

Yup , I missed that . Thanks .

 

[Fernando Revilla]

In general the first is not needed since it is already covered in the third condition

Not always. Previously we need to prove that $S\neq \emptyset$ (so, the best is to prove $0\in S$).

 

[chukkitty]

Dear All,

Thank you for your assistance.

I would try to prove two items to belong subspace or not. Because I don't know to write some Maths symbol on internet. So please refer to attachment of my work image.

(ITEM 1) The set contains the zero vector, as a=b=c=0 given p(x)=0+0x+0x².
Let p₁(x)=a₁+b₁x+c₁x² and p₂(x)=a₂+b₂x+c₂x².
Then p₁(x)+p₂(x)=(a₁+a₂)+(b₁+b₂)x+(c₁+c₂)x²
This polynomial has the correct form for a vector in U, so U is closed under vector addition.
Let p(x)=a+bx+cx² and α=ℝ and a,b,c∈ℚ.
Then αp(x)=(αa)+(αb)x+(αc)x²
This vector does not have the correct form for a vector in U if α can be irrational number, so U is not closed under scalar multiplication.
A counter-example: p(x)=(1/7)+(2/(11))x+(5/3)x²
Let α=√(13), then αp(x)=((√(13))/7)+((2√(13))/(11))x+((5√(13))/3)x². Show that the coefficients of x⁰,x¹,x² are not rational number. (ITEM 2) The set contains the zero vector, as b=0 and any c given p(x)=0x+0x².
Let p₁(x)=b₁x+cx² and p₂(x)=b₂x+cx²
p₁(x)+p₂(x)= (b₁+b₂)x+(2c)x², where any c
This polynomial has the correct form for a vector in P₂, so P₂ is closed under vector addition.

Let p(x)=bx+cx² and α=ℝ
Then αp(x)=(αb)x+(αc)x² , where any c
This polynomial has the correct form for a vector in P₂, so P₂ is closed under scalar multiplication.
So P₂ is a subspace of P₃.

Please give me advise.

Thank you very much!

Kitty