Proving $T(n)=\Theta(n \log n)$ by Induction

  • MHB
  • Thread starter evinda
  • Start date
  • Tags
    Induction
In summary, the conversation is about a recurrence relation where the goal is to prove that it is of the order $\Theta(n \log n)$. The base case for the proof by induction is $n=5$.
  • #1
evinda
Gold Member
MHB
3,836
0
Hi! (Nerd)

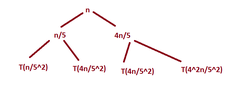
I am looking at the following recurrence relation: $T(n)=T \left( \frac{n}{5} \right)+T\left( \frac{4n}{5}\right)+n$.

The recurrence tree has this form:

View attachment 3620

So, we see that $T(n)=\sum_{j=0}^{\log_5(4n)} n=n \left( \log_5(4n)+1\right)$

Now, I want to prove by induction that $T(n)=\Theta(n \log n)$.

For which number do I have to show that the base case holds? (Thinking)
 

Attachments

  • extree.png
    extree.png
    2.4 KB · Views: 67
Physics news on Phys.org
  • #2
The base case is usually the smallest value of $n$ in the recurrence relation. In this case, that would be $n=5$. Therefore, we have to show that $T(5)=\Theta(5 \log 5)$.
 

FAQ: Proving $T(n)=\Theta(n \log n)$ by Induction

What is the general process for proving $T(n)=\Theta(n \log n)$ by induction?

The general process for proving $T(n)=\Theta(n \log n)$ by induction involves three steps:

  1. Proving the base case, typically for $n=1$ or $n=0$
  2. Assuming that the statement is true for some value $k$
  3. Using this assumption to prove that the statement is also true for $k+1$
Once these three steps have been completed, the induction proof is considered complete and the statement is proven to hold true for all values of $n$.

Why is the base case important in proving $T(n)=\Theta(n \log n)$ by induction?

The base case is important because it serves as the first step in the induction proof. It establishes that the statement holds true for the smallest possible value of $n$, and serves as a starting point for the rest of the proof. Without a valid base case, the induction proof cannot be completed and the statement cannot be proven to hold true for all values of $n$.

What is the difference between proving $T(n)=\Theta(n \log n)$ by strong induction vs. regular induction?

The main difference between strong induction and regular induction is the number of assumptions that are made. In regular induction, only one assumption is made about the statement holding true for a particular value of $n$ in order to prove the statement for the next value. In strong induction, multiple assumptions are made about the statement holding true for different values of $n$, providing a stronger base for the proof.

Can $T(n)=\Theta(n \log n)$ be proven using weak induction?

No, $T(n)=\Theta(n \log n)$ cannot be proven using weak induction. Weak induction only allows for one assumption to be made about the statement holding true for a particular value of $n$, which is not enough to prove the statement for all values of $n$. Strong induction is required in order to prove $T(n)=\Theta(n \log n)$.

What are the common mistakes to avoid when proving $T(n)=\Theta(n \log n)$ by induction?

Some common mistakes to avoid when proving $T(n)=\Theta(n \log n)$ by induction include:

  • Not properly establishing the base case
  • Making incorrect assumptions about the statement
  • Not using the assumption(s) to prove the statement for the next value of $n$
  • Not clearly stating the induction hypothesis
  • Not including all necessary steps and explanations in the proof
It is important to carefully follow the steps of induction and to be thorough and clear in the proof in order to avoid these mistakes.

Similar threads

MHB Binomial Distribution: Likelihood Ratio Test for Equality of Several Proportions
Replies
1
Views
3K
MHB Master Theorem-Relation of the two functions
Replies
2
Views
972
MHB Can We Prove the Inductive Set Contains Only Natural Numbers?
Replies
10
Views
1K
Chernoff Bounds using importance sampling identity
Replies
0
Views
1K
MHB Calculate the density - Unbiased estimator for θ
Replies
1
Views
1K
MHB Proving by Induction: Solving Recurrence Relation
Replies
5
Views
2K
I Randomly Stopped Sums vs the sum of I.I.D. Random Variables
Replies
2
Views
2K
MHB Upper Bound for Recurrence Relation: $T(n) \leq c n^2 \log^2 n$
Replies
6
Views
2K
MHB Probability to get a chocolate snowman or a chocolate reindeer
Replies
2
Views
1K
MHB Proving $T(2^k)=2^k \cdot k$ with Induction
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top