Proving the result of the following limit

[Rikudo]

Homework Statement

Proving value of this limit. (see the picture below)

Relevant Equations

euler's limit identity

Right now, I am trying to prove this :

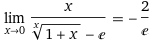
I tried to use this identity to solve it:

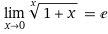
Then, the limit will become $\frac {x}{e-e}$
However, the result is still $\frac 0 0$

Could you please give me hints to solve this problem?

 

[nuuskur]

We are effectively computing derivative at $t=0$ by definition for $f(x) := (1+x)^{1/x}$
$$\lim _{x\to 0} \frac{f(x)-f(0)}{x} = \lim _{x\to 0} \frac{(1+x)^{1/x} - e}{x}$$
The map $f$ is differentiable since it's a composition of differentiable maps (i.e the above limit exists). Expressions of the form $\frac{d}{dx}a(x)^{b(x)}$ can be tackled with logarithmic differentiation.

Seems like a fancy way of saying "use L'Hopital's rule".

 

[Rikudo]

We are effectively computing derivative at $t=0$ by definition for $f(x) := (1+x)^{1/x}$
$$\lim _{x\to 0} \frac{f(x)-f(0)}{x} = \lim _{x\to 0} \frac{(1+x)^{1/x} - e}{x}$$
The map $f$ is differentiable since it's a composition of differentiable maps (i.e the above limit exists). Expressions of the form $\frac{d}{dx}a(x)^{b(x)}$ can be tackled with logarithmic differentiation.

Seems like a fancy way of saying "use L'Hopital's rule".

Ok. so, I tried to differentiate the $(1+x)^{1/x}$, and using the rule, I get:

$$\lim _{x\to 0} \frac{x}{(1+x)^{1/x} - e} = \frac{1}{\frac{x(1+x)^{-1+\frac{1}{x}}\,\,-\,\,(1+x)^{\frac 1 x}\,\,ln(1+x)}{x^2}}$$

Then, all I need to do is to substitute the value of $x$ as zero, right?
The answer is quite strange...The denominator will be $\frac 0 0$

 

[anuttarasammyak]

Your denominator is
$$\lim_{x \rightarrow 0}(1+x)^{\frac{1}{x}}[\frac{1}{x}(1- \ln (1+x)^{\frac{1}{x}})-\frac{1}{1+x}]$$
$$=e \lim_{x \rightarrow 0}[\frac{1}{x}(1- \ln (1+x)^{\frac{1}{x}})-1]$$
Maclaulin expansion formula of log (1+x) seems helpful for investigation of this limit.

 

[Rikudo]

Maclaulin expansion formula of log (1+x) seems helpful for investigation of this limit.

Ah. I see.. Now I managed to prove it.

There are some things that is bothering me,though..
1. Why my method in post 1 does not work?

2. I tried a different way to transform the term $ln(1+x)$, but I only get the first term of the maclaurin series.
Here is what I did:
let $y= ln(1+x)$

Then, we can rewrite this equation as $$e^y=(1+x)$$
Now, since x->0, we can use the identity of euler number
$$e^{\frac y x}= (1+x)^{\frac 1 x} $$
$$e^{\frac y x} = e$$
$$y = ln(1+x) = x $$
As we can see, this result slightly different from the maclaurin's ($x-\frac {x^2}{2}$)

 

[anuttarasammyak]

1.$$\frac{x^2}{x},\frac{x}{x},\frac{x}{x^2}$$
are all 0/0. We need to investigate orders to zero in denominator and numerator to get the limit value. L'Hopital rule is a popular one to do it.
2.$$y(x)=\ln (1+x)$$
$$y(0)=0$$
$$y^{(1)}(x)=\frac{1}{1+x}$$
$$y^{(1)}(0)=1$$
$$y^{(2)}(x)=-\frac{1}{(1+x)^2}$$
$$y^{(2)}(0)=-1$$
Thus we get Taylor series of
$$y(x)=\ln (1+x)=x-\frac{x^2}{2}+...$$

 

[nuuskur]

I would write $f(x) = \exp (\ln(1+x)/x)$. Then
$$f'(x) = (1+x)^{1/x}\left (\frac{1}{x^2+x} - \frac{1}{x^2}\ln (1+x) \right ) \xrightarrow[x\to 0]{} - \frac{e}{2}$$
The right term converges to $-\frac{1}{2}$ so the result follows.

Ok. so, I tried to differentiate the $(1+x)^{1/x}$, and using the rule, I get:

$$
\lim _{x\to 0} \frac{x}{(1+x)^{1/x} - e} = \frac{1}{\frac{x(1+x)^{-1+\frac{1}{x}}\,\,-\,\,(1+x)^{\frac 1 x}\,\,ln(1+x)}{x^2}}
$$

Then, all I need to do is to substitute the value of $x$ as zero, right?
The answer is quite strange...The denominator will be $\frac 0 0$

Write $\lim_ {x\to 0}$ on the RHS as well (the derivative is incorrect, though). Substitution might work, but doesn't have to. In the event of "$\frac{0}{0}$", apply L'Hopital.

 

[Rikudo]

We are effectively computing derivative at $t=0$ by definition for $f(x) := (1+x)^{1/x}$
$$\lim _{x\to 0} \frac{f(x)-f(0)}{x} = \lim _{x\to 0} \frac{(1+x)^{1/x} - e}{x}$$

Why can't we just substitute $(1+x)^{1/x}$ as $e?$

then, this equation will become:
$$\lim _{x\to 0} \frac{f(x)-f(0)}{x} = \lim _{x\to 0} \frac {e- e}{x}$$
Since x is near zero, then we can make it like this:
$$\lim _{x\to 0} \frac{f(x)-f(0)}{x} = \lim _{x\to 0} \frac{0}{x}$$
So, the answer to this limit equation which I have quoted from your reply is $0$

 

[pasmith]

You can assume $|x| < 1$ and expand $(1 + x)^{1/x}$ as a binomial expansion:
$$\begin{split} \frac{(1 + x)^{1/x} - e}{x} &= \frac{1}{x}\left( 1 - e + \sum_{n=1}^\infty \frac{x^n}{n!} \prod_{k=0}^{n-1} \left( \frac 1x - k \right) \right) \\ &= \frac{1}{x} \left(2 - e + \sum_{n=2}^\infty \frac{1}{n!} \prod_{k=1}^{n-1} (1 - kx) \right) \end{split}.$$ The only terms you need from $\prod_{k=1}^{n-1} (1 - kx)$ are the O(1) and O(x) terms; everything else will vanish in the limit $x \to 0$.

 

[nuuskur]

Why can't we just substitute $(1+x)^{1/x}$ as $e?$

then, this equation will become:
$$\lim _{x\to 0} \frac{f(x)-f(0)}{x} = \lim _{x\to 0} \frac {e- e}{x}$$
Since x is near zero, then we can make it like this:
$$\lim _{x\to 0} \frac{f(x)-f(0)}{x} = \lim _{x\to 0} \frac{0}{x}$$
So, the answer to this limit equation which I have quoted from your reply is $0$

Alright, I'll bite. You claim that the derivative of every differentiable function at $0$ is equal to $0$. That's obviously false.

You can't just limit the expression piece by piece. It's not valid in general. While it is true that $\lim _{x\to 0} f(x)-e =0$, the quantity $\frac{1}{x}$ is not bounded as $x\to 0$. So you can't claim the limit of the whole thing is zero.

Your argument is akin to claiming something like
$$\lim _{x\to\infty} \left ( 1+\frac{1}{x} \right )^x = \lim _{x\to\infty} 1^x = 1 .. \quad\text{(this is false!)}$$
it doesn't work like that.

 

[Mark44]

Why can't we just substitute $(1+x)^{1/x}$ as $e?$

Because they're not equal. The limit of the first expression, as x approaches zero, is the number e.

Your argument is akin to claiming something like $$\lim _{x\to\infty} \left ( 1+\frac{1}{x} \right )^x = \lim _{x\to\infty} 1^x = 1 .. \quad\text{(this is false!)}$$

What he said.
The limit above is another indeterminate form; namely $[1^\infty]$. It's indeterminate because limits of this form can have arbitrary values.