- #1
anemone
Gold Member
MHB
POTW Director
- 3,883
- 115
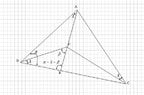
Inside a triangle $ABC$, there is a point P satisfies $\angle PAB=\angle PBC=\angle PCA=\lambda$. If the angles of the triangle are denoted by $\alpha$, $\beta$ and $\gamma$, prove that
$\dfrac{1}{\sin^2 \lambda}=\dfrac{1}{\sin^2 \alpha}+\dfrac{1}{\sin^2 \beta}+\dfrac{1}{\sin^2 \gamma}$
$\dfrac{1}{\sin^2 \lambda}=\dfrac{1}{\sin^2 \alpha}+\dfrac{1}{\sin^2 \beta}+\dfrac{1}{\sin^2 \gamma}$