Proving well ordering principle from Peano Axioms

[issacnewton]

Homework Statement

Let $G \subseteq \mathbb{N}$ be a non empty set. Then there is some $m \in G$ such that $m \leq g$ for all $g \in G$

Relevant Equations

Peano Axioms where lowest element is taken to be 1.

I am trying to understand the proof given in Ethan Bloch's book "The real numbers and real analysis". I am posting snapshot of the proof in the book.

I am also posting theorem 1.2.9 given in the book.

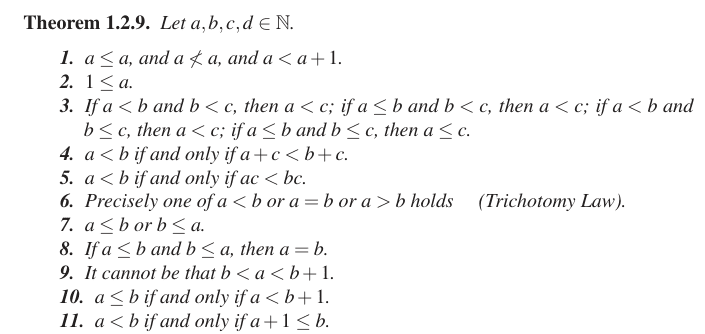
Here author is trying proof by contradiction. First, I don't understand why specific choice of the set $H$ was done. Is there any hint in the statement of the theorem 1.2.10 that this set needs to be considered. Next, the author is using contradiction at 3 different places in the proof. Though I am following what he says, but is this usual in math proofs to use contradiction at several places ? When I studied the method of proof by contradiction, there is only one contradiction at the end. So, this was new way to do proofs to me. Finally, when author states at the end that $H = \mathbb{N}$, how does theorem's statement follow ?

 

[FactChecker]

Here author is trying proof by contradiction. First, I don't understand why specific choice of the set $H$ was done.

$H \subseteq \mathbb{N}$ is the set of all possible lower limits for the set $G$. For a proof by contradiction, it was assumed that $H \cap G = \phi$.

Is there any hint in the statement of the theorem 1.2.10 that this set needs to be considered.

Yes. The theorem implies that $H \cap G \ne \phi$.

Next, the author is using contradiction at 3 different places in the proof. Though I am following what he says, but is this usual in math proofs to use contradiction at several places ?
When I studied the method of proof by contradiction, there is only one contradiction at the end. So, this was new way to do proofs to me.

I think he is just stating things that the assumption for a contradiction implies about $H$. It implies several things that take some thought to establish.

Finally, when author states at the end that $H = \mathbb{N}$, how does theorem's statement follow ?

Because if $H = \mathbb{N}$ and $H \cap G = \phi$ and $G \subseteq \mathbb{N}$, then $G = \phi$, which contradicts an assumption of the theorem.

 

[issacnewton]

Thanks.

 

[mathwonk]

If it makes you feel any better, I am a retired professional mathematician, and although I can follow that proof, I think it is one of the most complicated proofs I have seen in a supposedly elementary book. With apologies to Ethan, I myself would possibly toss this book on the strength of that one example of its marginal usefulness.

Out of fairness, this is probably an example of why it is not always helpful for understanding, to try to deduce everything from a minimal set of axioms, and perhaps not Prof. Bloch's fault. However Factchecker's nice enhancement shows it could have been made much more clear.

In fact I would have defined H (without negations) as all a such that if n is in N and in G, then n ≥ a. Then H really is the set of all lower bounds for G, and all we have to do is show that G does meet H. So assume G is non empty but disjoint from H, and derive a contradiction. This time the fact that 1 is in H is immediate from Theorem 1.2.9(2), no argument needed. Now if G is non empty but disjoint from H, then H is not everything, so by Peano (negated) there is some a in H (and in N) with a+1 not in H. Then (as in Bloch's argument) there is some p in G with a ≤ p < a+1), hence p = a is in both G and H; we are done by contradiction since then G is in fact not disjoint from H.

A good exercise might be to write up the proof for yourself with as few negations as possible.

 

[issacnewton]

Ok. I think I can put your arguments together and following is my proof. Let $H$ be defined as follows

$$H = \Bigl\{a \in \mathbb{N} \;| \forall n \in \mathbb{N}\; (n \in G \to n \geqslant a) \Bigr \} $$

Now, for arbitrary $n \in \mathbb{N}$, suppose that $n \in G$. Since $n \in \mathbb{N}$, it follows from Theorem 1.2.9(2), that $n \geqslant 1$. So, it follows that

$$ \forall n \in \mathbb{N} \;(n \in G \to n \geqslant 1) $$

and, since $1 \in \mathbb{N}$, we have that $1 \in H$. Now, assume that $H \cap G = \varnothing$. Now, since $G \subseteq \mathbb{N}$ is non empty and $H \cap G = \varnothing$, it means that $\exists x (x \in \mathbb{N}) \wedge (x \notin H)$. This means that $H \neq \mathbb{N}$. Using Peano postulates, taking contrapositive of induction hypothesis, we have

$$ (H \ne \mathbb{N}) \longrightarrow \Bigl[(1 \notin H) \vee \neg (h \in H \to (h+1) \in H) \Bigr] $$

But, since $H \neq \mathbb{N}$, using Modus ponens, we have

$$(1 \notin H) \vee \neg (h \in H \to (h+1) \in H) $$

converting this with implication, we have

$$ (1 \in H) \longrightarrow \neg (h \in H \to (h+1) \in H) $$

$$ (1 \in H) \longrightarrow (h \in H) \wedge (h + 1 \notin H) $$

But, since $1 \in H$, again using Modus ponens, we have , $(h \in H) \wedge (h + 1 \notin H)$. Now, $(h \in H)$ means that

$$\forall n \in \mathbb{N} \;(n \in G \to n \geqslant h) \cdots \cdots (1) $$

and $(h + 1 \notin H)$ means the negation

$$\exists n \in \mathbb{N} \; (n \in G) \wedge (n < h+1) $$

So, we have (using existential instantiation) $n \in \mathbb{N}$ and $n \in G$ and $n < h+1$. Since $h \in H$, using $(1)$, this means that $h \leqslant n$. Combining, we have $h \leqslant n < h+1$. But according to Theorem 1.2.9 (9), it can not be that $h < n < h+1$. This means that $h = n$. Since $h \in H$ and $n \in G$, we have an element which is common to both $G$ and $H$. So, $H \cap G \neq \varnothing$, which is a contradiction. This means that, our initial assumption that $H$ and $G$ are disjoint is false. So, let $m$ be the element which is common to both $H$ and $G$. And let $g\in G$ be an arbitrary element. Since $m \in H$, it follows that $m \leqslant g$. And $g$ is arbitrary, so, this proves that there is some $m \in G$ such that $m \leqslant g$ for all $g \in G$.

Do you think this is a valid proof mathwonk ? $\smile$

 

[mathwonk]

Excellent, except to be picky, you have omitted some existential quantifiers, e.g. in line minus 17, it should say "there exists h such that". Of course also in line -16 there is an implied universal quantifier. nice work overall.

 

[issacnewton]

Awesome !!. I had studied the book "How to Prove It: A Structured Approach" by Daniel Velleman. He is a set theorist, so the language of the book is very precise. So, I am very comfortable with quantifiers. Proofs become easier to follow with them.

 

[mathwonk]

quantifiers are actually essential for precise statements. recall existential quantifiers affirm a statement for at least one element of a given set, while universal quantifiers do so for all such elements.
although it may sound otherwise, existential statements are often stronger than universal ones, since the given set may be empty, so that then "all" elements of it means actually no elements at all!
In your case for example, every element of (G meet H) is a lower bound for G which belongs to G, but we must still show there is one.

On another note, an error that often occurs in books is the attempt to prove that the well ordering principle implies the principle of induction. This is actually false, since there exist well ordered sets which contain proper subsets satisfying the inductive hypotheses.

I.e. reorder the positive integers so that all even numbers are larger than all odd numbers, and so that the successor function is adding 2 rather than adding 1. then the odd numbers do contain 1 and do contain the immediate successor of every element they contain; still they do not contain all elements. Nonetheless every non empty subset has a least element. The problem is that the element 2 in this new ordering has no immediate predecessor. A well ordered set in which every element has an immediate predecessor does satisfy the induction principle.

The usual incorrect argument that well ordering does imply inductive principle, is to take a subset containing 1 and containing the successor of every element, and try to argue that the complement is empty. If not, that complement has a least element x, and the contradiction is supposedly to consider the immediate precursor of x, but in our case, the element 2 has no immediate precursor in the new ordering.

Of course in the case of the positive integers, with their usual ordering, one can use this to show: if the positive integers satisfy well ordering then they also satisfy induction, since if x is the least element of the complement of an inductive set S of positive integers, then x-1 is also a positive integer, hence belongs to S. But then (x-1)+1 = x, also belongs to S, a contradiction unless the complement of S is empty. Even to give this proof, one must discuss the ability to subtract 1 from positive integers greater than 1.

 

[nuuskur]

Alternatively, the claim can be proved by induction. Part of the reason why the given proof gets so "weird" is because PA does not really lend itself nicely to nonconstructive arguments.

Let $X$ be a nonempty subset. If it contains $0$, then we're done. Suppose every nonempty subset that contains at least one element up to $n$ has smallest element. Let $X$ be a subset containing $n+1$. If it contains anything smaller than $n+1$, then we're done by assumption. Otherwise, $n+1$ is the smallest element.

On another note, an error that often occurs in books is the attempt to prove that the well ordering principle implies the principle of induction. This is actually false, since there exist well ordered sets which contain proper subsets satisfying the inductive hypotheses.

Yes, in general the claim is false - we can't perform induction on something like polynomials with coefficients in $\mathbb N$, but the set is nonetheless well ordered.

 

[Erland]

How does Bloch define $\le$ for natural numbers? I noticed that he used his theorem to prove $1\le n$ for all $n \in \Bbb N$, but by any reasonable definition of $\le$, this should be trivial to prove, and then Theorem 1.2.10 would be trivial.