Puck collision with rod using angular momentum conservation

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

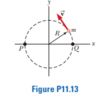
For this problem,

Why for part (a) the solution is,

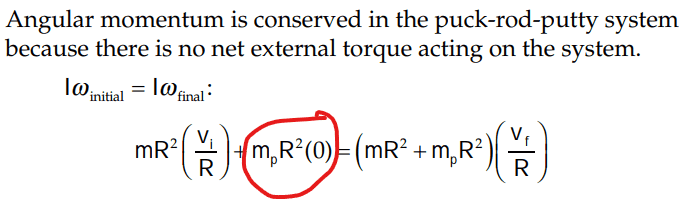
Is the bit circled in red zero because since the putty is released at a very small distance above the rod it velocity is negligible?

Also for part (d) the solution is

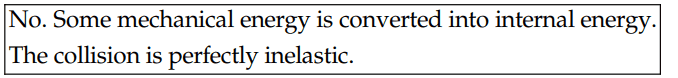
I did a computation of the initial and finial kinetic energies of the system and found:

$KE_f = \frac {KE_im_i} {2m_f}$ so I guess that's why the finial KE is less than the initial.

Many thanks!

 

[DrClaude]

Is the bit circled in red zero because since the putty is released at a very small distance above the rod it velocity is negligible?

The putty has no velocity component in the plane of rotation, so its initial angular velocity is 0. The fact that it is released a small distance above the puck allows to neglect what happens out of the plane.

 

[kuruman]

I did a computation of the initial and finial kinetic energies of the system and found:

$KE_f = \frac {KE_im_i} {2m_f}$ so I guess that's why the finial KE is less than the initial.

The final KE is indeed less than the initial but twice as much as what you have.

 

[member 731016]

The putty has no velocity component in the plane of rotation, so its initial angular velocity is 0. The fact that it is released a small distance above the puck allows to neglect what happens out of the plane.

Thank you for your reply @DrClaude!

Sorry, what do you mean by the putty has no velocity component in the plane of rotation?

I've tried to draw it out:

Since the problem does not specify where the putty is dropped onto the puck during the rotation, I thought that if it was dropped during the second quadrant of motion, such as when the puck is at point P, then it would have vertical velocity exactly in the direction of the puck's tangential velocity?

The fact that it is released a small distance above the puck allows to neglect what happens out of the plane.

Is you second statement about neglecting what happens out of the plane referring to the fact that the problem states that the putty is dropped a very small distance above the puck then when we can neglect its vertical velocity?

Many thanks!

 

[member 731016]

The final KE is indeed less than the initial but twice as much as what you have.

Thank you for your reply @kuruman ! I found my mistake :)

 

[nasu]

The motion is in a horizontal plane. The putty is dropped vertically. It looks like you misunderstand the situation.

 

[member 731016]

The motion is in a horizontal plane. The putty is dropped vertically. It looks like you misunderstand the situation.

Thank you for you reply @nasu! Oh I think I understand now. So the putty is dropped in the z-direction, I though it was dropped in the y-direction for some reason.

Since it is dropped in the z-direction then it does not matter whether it has a non-zero velocity in the z-direction since the force applied will be only in the z-direction so angular momentum must be conserved since $\tau = \vec F \times \vec r = 0$

 

[kuruman]

Since it is dropped in the z-direction then it does not matter whether it has a non-zero velocity in the z-direction since the force applied will be only in the z-direction so angular momentum must be conserved since $\tau = \vec F \times \vec r = 0$

You have to be careful here. Saying "the angular momentum must be conserved" is not enough. You need to specify the system and the axis of rotation. Here the axis of rotation is obvious. What do you think the system is that has its angular momentum unchanged? Also, your expression $\tau = \vec F \times \vec r = 0$ is an insufficient explanation why angular momentum is conserved.

 

[member 731016]

You have to be careful here. Saying "the angular momentum must be conserved" is not enough. You need to specify the system and the axis of rotation. Here the axis of rotation is obvious. What do you think the system is that has its angular momentum unchanged? Also, your expression $\tau = \vec F \times \vec r = 0$ is an insufficient explanation why angular momentum is conserved.

Thank you for your reply @kuruman!

I think angular momentum is conserved for the puck and putty system.

I tried to do find a different expression for $\tau$ so
$\tau = \vec F \times \vec R$
$\tau = FR\sin\theta$
$\tau = FR\sin90$ (since force into plane of rotation and displacement vector makes 90 degree angle with line of action)
$\tau = FR$

....so it looks I have just memorized the insufficient $\tau = \vec F \times \vec r = 0$ explanation.

I think since the $\tau$ is perpendicular to $\vec v$ for every $\vec R$ and there is a normal force $\vec N$ from the ground (that provides and equal and opposite torque) so angular momentum is conserved?

I also tried to do it with vector components, however, I'm not too sure how to prove that angular momentum is conserved from here.
$\tau = F\hat {(-k)} \times \vec R$
$\tau = -F\hat k \times (x\hat i + y\hat j)$
$\tau = F\hat j - F\hat i$

Many thanks!

 

[kuruman]

Forces are generated by entities and exerted on other entities called "systems". Note that these forces are external to the systems on which they act. Now here you chose the puck + putty system. That's fine. What entity generates the external force $F(-\hat k)$ that you wrote down? I want to make that you understand how this is put together. You probably noticed that the torque you wrote down, $\tau = F\hat j - F\hat i$, is not zero unless $F$ is zero.

 

[member 731016]

Forces are generated by entities and exerted on other entities called "systems". Note that these forces are external to the systems on which they act. Now here you chose the puck + putty system. That's fine. What entity generates the external force $F(-\hat k)$ that you wrote down? I want to make that you understand how this is put together. You probably noticed that the torque you wrote down, $\tau = F\hat j - F\hat i$, is not zero unless $F$ is zero.

Thank you for your reply @kuruman !

I think the force $F(-\hat k)$ would be an internal force pair to putty-puck system generated by Newton's Third Law.

However, if the puck is the system, then $F(-\hat k)$ is an external force from the collision.

Many thanks!

 

[kuruman]

I think the force $F(-\hat k)$ would be an internal force pair to putty-puck system generated by Newton's Third Law.

However, if the puck is the system, then $F(-\hat k)$ is an external force from the collision.

Many thanks!

If the system is the puck, then there is an external torque exerted by the putty that changes the puck's angular momentum about its axis of rotation is not conserved. The angular momentum of the putty about the same axis is also not conserved because initially it is not rotating about that axis but after the collision it is.

Here we are looking for an argument why the angular momentum of the puck + putty system in the $\hat k$ direction is conserved, i.e. it is the same before and after the collision. Look at the two items that make up the system. What is the net external force acting on it? What is the net external torque acting on it?

 

[member 731016]

If the system is the puck, then there is an external torque exerted by the putty that changes the puck's angular momentum about its axis of rotation is not conserved. The angular momentum of the putty about the same axis is also not conserved because initially it is not rotating about that axis but after the collision it is.

Here we are looking for an argument why the angular momentum of the puck + putty system in the $\hat k$ direction is conserved, i.e. it is the same before and after the collision. Look at the two items that make up the system. What is the net external force acting on it? What is the net external torque acting on it?

Thank you for your reply @kuruman !

So if the puck + putty is the system, then the horizontal surface and earth is external to the system. So the external forces acting on the puck and putty system is gravity and the normal force. I assume that the earth as infinite inertia, so when the putty collides with the puck is stops with an infinite acceleration from an infinite normal force. I don't think there is a net external torque because during the collision there is no movement of the puck and putty system in the $\hat k$ direction.

Many thanks!

 

[kuruman]

I don't think there is a net external torque because during the collision there is no movement of the puck and putty system in the k^ direction.

The question is not whether angular momentum is conserved instantaneously at the moment of th collision. The question is: Is the angular momentum of the puck + putty system conserved from the moment the putty is released until after it stuck to the puck and moves as one with it? The answer is subtle.

 

[member 731016]

The question is not whether angular momentum is conserved instantaneously at the moment of th collision. The question is: Is the angular momentum of the puck + putty system conserved from the moment the putty is released until after it stuck to the puck and moves as one with it? The answer is subtle.

Thank you @kuruman for your reply!

It looks like I answered whether angular momentum is conserved during the collision in post #13. So, I will answer whether angular momentum is conserved before and after the collision.

I don't think angular momentum is conserved while the putty is in free fall.

Angular momentum is conserved after the collision because gravity and normal force balance acting on the combined object.

Many thanks!

 

[kuruman]

Thank you @kuruman for your reply!

It looks like I answered whether angular momentum is conserved during the collision in post #13. So, I will answer whether angular momentum is conserved before and after the collision.

I don't think angular momentum is conserved while the putty is in free fall.

Angular momentum is conserved after the collision because gravity and normal force balance acting on the combined object.

Many thanks!

Not so fast. Remember that every time you mention angular momentum you have to specify the axis about which this angular momentum is to considered. The two questions below refer to the situation where the putty is falling through the air before the collision. Assume that position of the putty relative to the center of the puck is described by the equation $$\mathbf{r}=R~\mathbf{\hat i}+(h-\frac{1}{2}gt^2)~\mathbf{\hat k}.$$For the two-component system puck + putty:
Question 1: What are the three components of the torque due to gravity relative to the center of the puck?
Question 2: What are the three components of the angular momentum relative to the center of the puck?

 

[member 731016]

Not so fast. Remember that every time you mention angular momentum you have to specify the axis about which this angular momentum is to considered. The two questions below refer to the situation where the putty is falling through the air before the collision. Assume that position of the putty relative to the center of the puck is described by the equation $$\mathbf{r}=R~\mathbf{\hat i}+(h-\frac{1}{2}gt^2)~\mathbf{\hat k}.$$For the two-component system puck + putty:
Question 1: What are the three components of the torque due to gravity relative to the center of the puck?
Question 2: What are the three components of the angular momentum relative to the center of the puck?

Thank you for your reply @kuruman ! Thanks for pointing that out the axis which I am considering torque and angular momentum is the z-axis in the $\hat k$ direction.

Solution 1:
$\tau = m\vec g \times \vec r$
$\tau = -mg \hat j \times [R \hat i + (h-\frac{1}{2}gt^2) \hat k]$
$\tau = mgR \hat k - (h-\frac{1}{2}gt^2) \hat i$

The three components of the $\tau_g = - (h-\frac{1}{2}gt^2) \hat i + 0\hat j + mgR \hat k$

Solution 2:
$\vec L = \int_0^t \tau \, dt$
$\vec L = \int_0^t mgR \hat k - (h-\frac{1}{2}gt^2) \hat i \, dt$
$\vec L = \int_0^t mgR \hat k - h \hat i + \frac{1}{2}gt^2 \hat i \, dt$
$\vec L = mgRt \hat k- ht \hat i + \frac {1}{6}gt^3 \hat i$

The three components of the $\vec L_g = (- ht + \frac {1}{6}gt^3) \hat i + 0\hat j + mgRt \hat k$
Many thanks!

 

[kuruman]

Try again. Look at the expression for the position vector. What is the direction of the acceleration? The force of gravity is in the same direction.

Also, if you use $\vec L=m\vec r\times \vec v$, you don't have to integrate. Just find the velocity vector $\vec v$ of a free falling body that starts from rest.

 

[member 731016]

Try again. Look at the expression for the position vector. What is the direction of the acceleration? The force of gravity is in the same direction.

Also, if you use $\vec L=m\vec r\times \vec v$, you don't have to integrate. Just find the velocity vector $\vec v$ of a free falling body that starts from rest.

Thank you for your reply @kuruman ! Sorry I'll fix that up, I forgot $\vec F = -mg\hat k$ for the coordinate system we were given!

 

[member 731016]

Here is the new version @kuruman

Solution 1:
$\tau = m\vec g \times \vec r$
$\tau = -mg \hat k \times [R \hat i + (h-\frac{1}{2}gt^2) \hat k]$
$\tau = -mgR \hat j$

Solution 2:
$\vec L= m\vec r\times \vec v$
$\vec L= -m[R \hat i + (h-\frac{1}{2}gt^2) \hat k]\times -gt\hat k$
$\vec L= -mRgt \hat j$

Thank you!

 

[kuruman]

Solution 1:
$\tau = m\vec g \times \vec r$

When you write cross products the order matters as you know. Also, torque is a vector. You should write
$\vec{\tau}=\vec r \times \vec F=\vec r\times (-mg~\hat k).$ That will change only the sign of the final result.

So the torque about the center of the puck on the putty is not zero and the putty's angular momentum about the center of the puck is not constant because it depends on time. However the torque is consistent with the equation $~\vec {\tau}=\dfrac{d\vec L}{dt}.$

So much for the putty. What about the puck? What is the angular momentum of the puck before the collision? Write that down and then write down the total angular momentum of the puck + putty system before the collision. Then you will see where I'm going with this.

 

[member 731016]

Thank you for your reply @kuruman !

When you write cross products the order matters as you know. Also, torque is a vector.

Sorry I did not realize I mixed up the order!

You should write
$\vec{\tau}=\vec r \times \vec F=\vec r\times (-mg~\hat k).$ That will change only the sign of the final result.

So the torque about the center of the puck on the putty is not zero and the putty's angular momentum about the center of the puck is not constant because it depends on time. However the torque is consistent with the equation $~\vec {\tau}=\dfrac{d\vec L}{dt}.$

So much for the putty. What about the puck? What is the angular momentum of the puck before the collision? Write that down and then write down the total angular momentum of the puck + putty system before the collision. Then you will see where I'm going with this.

Taking the angular momentum of the puck about the z-axis,

$\vec L = m\vec r \times \vec v$
$\vec L = m(x\hat i + y\hat j) \times (v_x\hat i + v_y\hat j)$
$\vec L = mxv_y \hat k - myv_x \hat k$

Therefore the angular momentum of the system is

$\vec L= -mRgt \hat j + mxv_y \hat k - myv_x \hat k$

Many thanks!

 

[member 731016]

When you write cross products the order matters as you know. Also, torque is a vector. You should write
$\vec{\tau}=\vec r \times \vec F=\vec r\times (-mg~\hat k).$ That will change only the sign of the final result.

So the torque about the center of the puck on the putty is not zero and the putty's angular momentum about the center of the puck is not constant because it depends on time. However the torque is consistent with the equation $~\vec {\tau}=\dfrac{d\vec L}{dt}.$

So much for the putty. What about the puck? What is the angular momentum of the puck before the collision? Write that down and then write down the total angular momentum of the puck + putty system before the collision. Then you will see where I'm going with this.

So where are you going with this @kuruman ? I have found the angular momentum of the puck + putty system before the collision in post #22.

Many thanks!

 

[kuruman]

So where are you going with this @kuruman ? I have found the angular momentum of the puck + putty system before the collision in post #22.

Many thanks!

Ah yes. This thread slipped my mind. Sorry for the delay.

Look at your expression for the angular momentum of the system before the collision and at the expression for the torque. Is angular momentum changing or not changing?

 

[member 731016]

Ah yes. This thread slipped my mind. Sorry for the delay.

Look at your expression for the angular momentum of the system before the collision and at the expression for the torque. Is angular momentum changing or not changing?

Thanks for your reply @kuruman ! No worries!

I think the angular momentum is changing because when I differentiate $\vec L$ it will give me $\vec \tau = mRg$ since $mxv_y \hat k - myv_x \hat k$ don't change with respect to time because x and y are functions of position not time and velocity is constant.

I guess x and y are also just equal to the distance from the origin along the x and y axes respectively which is always a number so is a constant.

Many thanks!

 

[kuruman]

I think the angular momentum is changing because when I differentiate L→ it will give me τ→=mRg since mxvyk^−myvxk^ don't change with respect to time because x and y are functions of position not time and velocity is constant.

OK, so if the angular momentum of the puck + rod + putty system is changing, that's another way to say that it is not conserved. How do you reconcile this conclusion with the opening statement in the given solution, "Angular momentum is conserved in the puck-rod-putty system because there is no external torque acting on the system"?

One of you is correct and one of you is wrong. Which is which? I will tell you what I think after you tell me what you think and why.

 

[member 731016]

OK, so if the angular momentum of the puck + rod + putty system is changing, that's another way to say that it is not conserved. How do you reconcile this conclusion with the opening statement in the given solution, "Angular momentum is conserved in the puck-rod-putty system because there is no external torque acting on the system"?

One of you is correct and one of you is wrong. Which is which? I will tell you what I think after you tell me what you think and why.

Thank you for your reply @kuruman !

I don't think angular momentum is conserved before the collision because there is a torque due to gravity acting on the putty.

I think the statement in the solution must be referring to during and after the collision.

I think during the collision the impact force from the putty on the puck will be equal to the normal force from the puck onto the putty. I think this is possible if the surface that the puck is on has infinite inertia, so will not accelerate during the collision but will exert a infinite force to slow the puck instantaneously. Since the net force is in the z-direction, then there must be a torque due to the normal force about the z-axis though plane of rotation. However, since this torque is perpendicular to the plane of rotation (and angular momentum of the puck), then it cannot change the puck's angular velocity and therefore angular momentum of the puck.

However, I now realize that during the collision, the putty will lose some of its angular momentum about the AoR. Does that mean that angular momentum is not conserved during the collision?

Maybe it's only a component of the angular momentum of the system putty + puck system that is conserved during before, during, and after the collision.

Many thanks!

 

[haruspex]

Thank you for your reply @kuruman !

I don't think angular momentum is conserved before the collision because there is a torque due to gravity acting on the putty.

I think the statement in the solution must be referring to during and after the collision.

I think during the collision the impact force from the putty on the puck will be equal to the normal force from the puck onto the putty. I think this is possible if the surface that the puck is on has infinite inertia, so will not accelerate during the collision but will exert a infinite force to slow the puck instantaneously. Since the net force is in the z-direction, then there must be a torque due to the normal force about the z-axis though plane of rotation. However, since this torque is perpendicular to the plane of rotation (and angular momentum of the puck), then it cannot change the puck's angular velocity and therefore angular momentum of the puck.

However, I now realize that during the collision, the putty will lose some of its angular momentum about the AoR. Does that mean that angular momentum is not conserved during the collision?

Maybe it's only a component of the angular momentum of the system putty + puck system that is conserved during before, during, and after the collision.

Many thanks!

This all seems to be getting unnecessarily complicated.
Note the wording of the question: the angular momentum of the puck-putty system about the axis of rotation…
Since gravity acts vertically, it has no torque about that axis.

Perhaps I'm missing a shift somewhere in the thread to considering the total angular momentum about the centre of rotation of the puck, just out of curiosity. But it is still no big deal.
When the putty hits the puck, there is a vertically upward impulse from the ground exactly matching the impulse gravity applied to the putty while it was falling. Thus, the total angular momentum of the system is suddenly restored to what it was before the putty was released.

 

[kuruman]

It may seem to be getting complicated because I was trying to get @Callumnc1 to see that the statement "Angular momentum is conserved in the puck-rod-putty system because there is no external torque acting on the system" is simply wrong and needed fixing. The fix is that there are torques acting on the system but not in the vertical direction which is what matters. Thus the vertical component of the system's angular momentum is the same before, during and after the collision. Initially @Callumnc1 thought that

I don't think there is a net external torque because during the collision there is no movement of the puck and putty system in the $\hat k$ direction.

is the justification for angular momentum conservation. That, I thought, revision preferably by @Callumnc1 with some guidance.

 

[haruspex]

Initially @Callumnc1 thought that

I don't think there is a net external torque because during the collision there is no movement of the puck and putty system in the k^ direction.

is the justification for angular momentum conservation.

Then here's my answer to that..
It's not whether there is movement but whether there is change of movement (acceleration). The putty’s movement changes considerably during the impact.

 

[member 731016]

Thank you for your replies @haruspex and @kuruman !

So since gravity is acting in the $\hat k$ direction means that the torque due to gravity on the putty is along the plane of rotation.

This means when the putty collides with the puck then the angular momentum of the puck in the $\hat k$ direction cannot be changed since the putty angular momentum dose not have component in the $\hat k$ direction since when it is falling is has angular momentum along the plane (in either the $\hat x$ or $\hat y$ direction or both) given by the right hand rule.

I see now that the solution should have specified that angular momentum is conserved in the $\hat k$ direction about the AoR. Now I see that they should have applied conservation of angular momentum in the $\hat k$ direction which is why the putty's angular velocity is zero.

Many thanks!

 

[haruspex]

the solution should have specified that angular momentum is conserved in the $\hat k$ direction about the AoR.

Why? "about the axis of rotation (of the puck)" implies the $\hat k$ direction.

 

[member 731016]

Why? "about the axis of rotation (of the puck)" implies the $\hat k$ direction.

Thank you for your reply @haruspex ! True it dose imply $\hat k$ direction.