Pulling down on the string connected to a whirling block on a table

[farfromdaijoubu]

Homework Statement

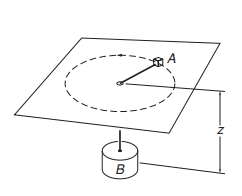
A horizontal frictionless table has a small hole in its centre. Block A on the table is connected to block B hanging beneath by a massless string which passes through the hole. Initially, B is held stationary and A rotates at constant radius R with constant angular velocity \omega If B is released at t=0, what is its acceleration immediately afterward?

Relevant Equations

$$T-m_ag = m_aa$$
$$T=m_b\omega^2R$$

At the time of release, the equation of motion of blocks A and B T-m_ag = m_aa and T=m_b\omega^2R respectively, where T is the tension in the string. Solving for the acceleration a then gives a=\frac{m_b\omega^2R - m_ag}{m_a}. Not sure what I did wrong or what incorrect assumptions I made here...

Thanks

 

[TSny]

Welcome to PF!

Relevant Equations:: T-m_ag = m_aa
T=m_b\omega^2R

Block $A$ is the block that is initially moving in a circle. Block $B$ is the hanging block. It looks like your subscripts $a$ and $b$ should be switched if $a$ is meant to refer to block $A$ and $b$ to block $B$.

A couple of things to consider:

(1) When block $B$ is released, the tension $T$ will "instantaneously" change from what it was just before $B$ was released. Just before $B$ is released, the tension is $m_a \omega^2 R$ because $A$ is moving in uniform circular motion before $B$ is released. But this will generally not be the tension just after $B$ is released.

(2) Block $A$ moves on a plane where polar coordinates would be appropriate for this problem. You might want to review how acceleration is expressed in polar coordinates. For example, see equation 4 here.