- #1
shivajikobardan
- 674
- 54
Please review my proof. Is this correct or not?

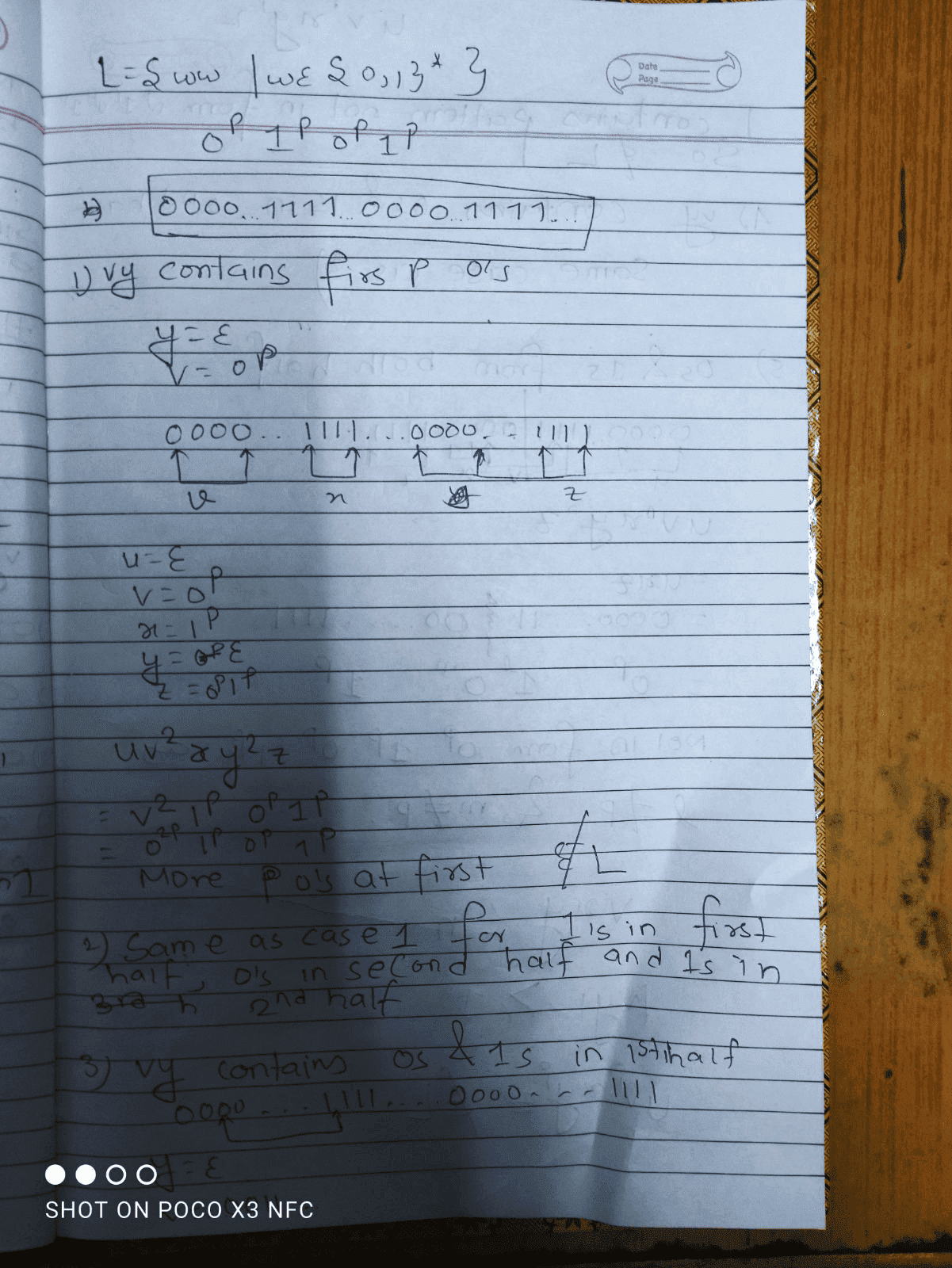
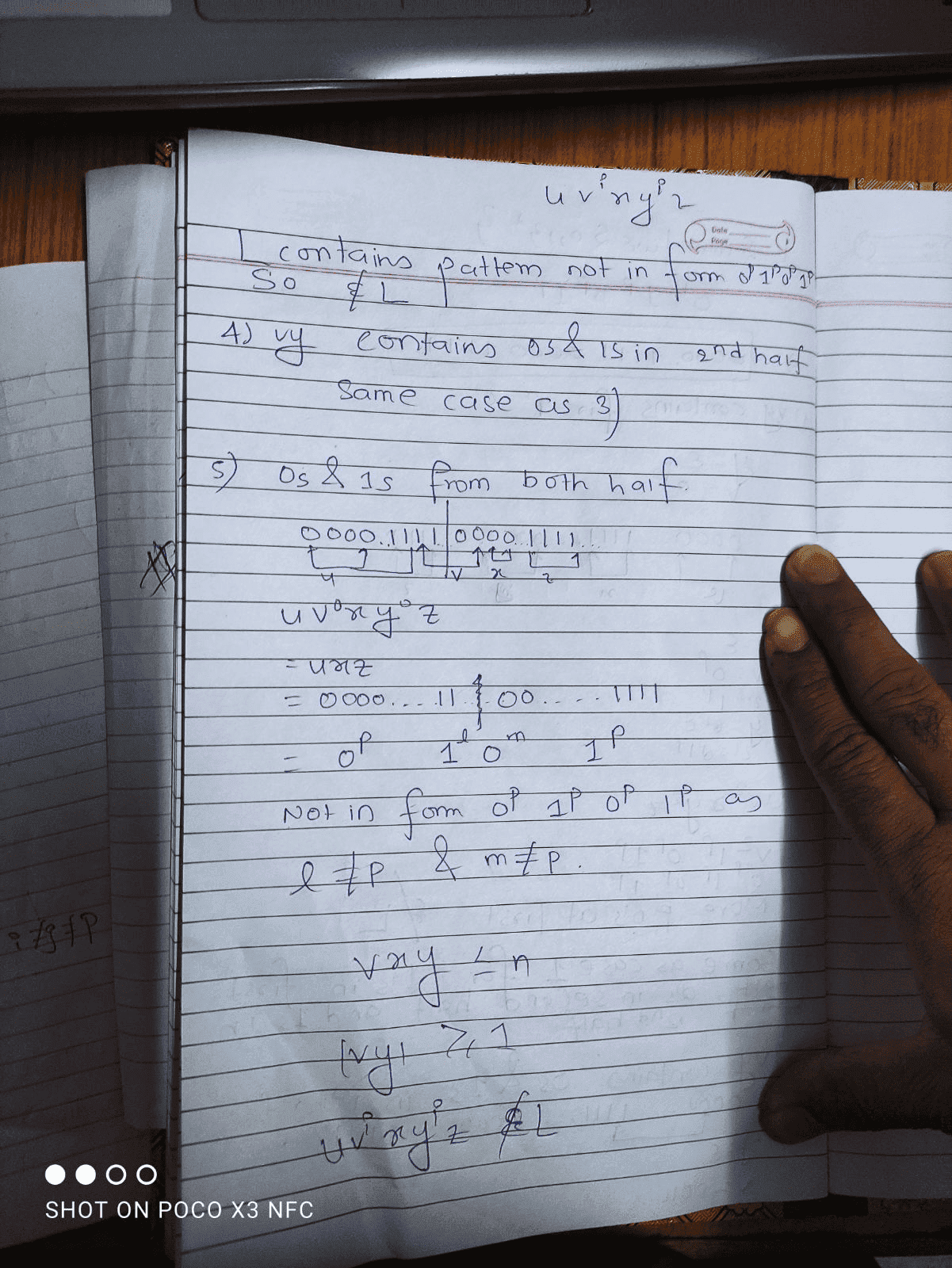
The Pumping Lemma is a theorem in formal language theory that helps to prove whether a given language is regular or not. It states that if a language L is regular, then there exists a constant number p (known as the "pumping length") where any string longer than p can be divided into three parts: uvw, such that v is non-empty, uvw is in L, and for any natural number n, uv^nw is also in L. In the case of L=0^p 1^p 0^p 1^p, this means that if the language is regular, there should exist a pumping length p where any string consisting of p 0's followed by p 1's followed by p 0's followed by p 1's can be pumped in the manner described above.
To prove that L is not regular, we must show that for any pumping length p, there exists a string in L that cannot be pumped. This can be done by assuming that L is regular and then using the Pumping Lemma to choose a string that cannot be pumped, leading to a contradiction. In the case of L=0^p 1^p 0^p 1^p, we can choose the string s=0^p 1^p 0^p 1^p and show that no matter how we divide it into uvw, we can always pump v or w in such a way that the number of 0's and 1's in the resulting string will not be equal, thus not satisfying the conditions of the language.
An example of a string that cannot be pumped in L=0^p 1^p 0^p 1^p is s=0000111100001111, where p=4. If we divide this string into uvw such that |v|=4, then v must contain at least one 0 and one 1, and thus pumping v would result in a string with an unequal number of 0's and 1's. Similarly, if we choose |v|=5, pumping w would result in an unequal number of 1's and 0's. Thus, this string cannot be pumped in a way that satisfies the conditions of the language.
No, the Pumping Lemma is not a sufficient condition for proving that a language is not regular. It only provides a necessary condition, meaning that if the conditions of the lemma are not satisfied, then the language is not regular. However, there are languages that do satisfy the conditions of the lemma but are not regular. Therefore, the Pumping Lemma should be used in conjunction with other methods and proofs to determine the regularity of a language.
Yes, the Pumping Lemma can be used to prove that a language is regular, but it is not the only method. It can be used to show that a language is not regular, but it cannot be used to prove that a language is regular. To prove that a language is regular, other methods such as constructing a regular expression or a finite automaton may be used.