- #1
lalahelp
- 75
- 0
Homework Statement
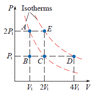
Suppose a monatomic ideal gas is changed from state A to state D by one of the processes shown on the PV diagram. (Let V1 = 4.80 L and P1 = 3.30 atm.)
(a) Find the total work done on the gas if it follows the constant pressure path A−E followed by the constant temperature path E−D.
(b)Calculate the total change in internal energy of the gas during the entire process.
(c)Calculate the total heat flow into the gas
2. W=pi(vf-vi)
(1.01e5)(3.3)(9.6-4.8)(.001)=1599.84 J
(1.01e5)(6.6+3.3)(19.2-9.6)(.001)= 4799.5 J
=6399 J
Why is my work wrong??