evinda
Gold Member
MHB
- 3,741
- 0
Hello! (Wave)
The solutions of $X^2+Y^2=Z^2$ are called Pythagorean Triples .
We suppose that $x$ odd and $y$ even.
All the solutions $(x,y,z)$ with $gcd(x,y,z)=1$ are given by:
$$(x,y,z)=(r^2-s^2,2rs,r^2+s^2)$$
$$r, s \in \mathbb{Z}, r>s, (r,s)=1$$
$$r \not\equiv s \pmod 2$$
Could you explain me why the following is the proof of the above sentence? (Sweating)
View attachment 3324
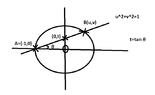
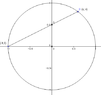
Line equation $AB$: $y-y_0=\lambda(x-x_0)$
so, $v=t(u+1)$.
Therefore, the point $B=(u,v)$ is a solution of the system:
$$\begin{Bmatrix}
u^2+v^2=1\\
v=t(u+1)
\end{Bmatrix}$$
Replacing $v$ at the first equation, we get:
$$(1+t^2)u^2+2t^2u+(t^2-1)=0$$
We solve the equation and find:
$$u=\frac{1-t^2}{1+t^2} , u=-1$$
$u=-1$ corresponds to the point $A=(-1,0)$.
We calculate $v=t(u+1)=\frac{2t}{t^2+1}$, so the coordinates of $B$ are:
$$B= \left ( \frac{1-t^2}{1+t^2}, \frac{2t}{1+t^2} \right )$$
Remark:
If the slope $t \in \mathbb{Q}$, then $B=(u,v) \in \mathbb{Q} \times \mathbb{Q}$.
Conversely, if the coordinates of $B=(u,v)$ are rational, then the line $AB$ has slope $t=\frac{v-0}{u+1} \in \mathbb{Q}$.
Therefore, the set of rational solutions of $x^2+y^2=1$ is:
$$\begin{Bmatrix}
(u,v)=\left ( \frac{1-t^2}{1+t^2}, \frac{2t}{1+t^2} \right )|t \in \mathbb{Q}
\end{Bmatrix} \cup \{ (-1,0)\}$$
Remark: If $t=\frac{r}{s}, r, s \in \mathbb{Z}, (r,s)=1$, we get the Pythagorean Triples.
But... how do we get them? (Sweating)
The solutions of $X^2+Y^2=Z^2$ are called Pythagorean Triples .
We suppose that $x$ odd and $y$ even.
All the solutions $(x,y,z)$ with $gcd(x,y,z)=1$ are given by:
$$(x,y,z)=(r^2-s^2,2rs,r^2+s^2)$$
$$r, s \in \mathbb{Z}, r>s, (r,s)=1$$
$$r \not\equiv s \pmod 2$$
Could you explain me why the following is the proof of the above sentence? (Sweating)
View attachment 3324
Line equation $AB$: $y-y_0=\lambda(x-x_0)$
so, $v=t(u+1)$.
Therefore, the point $B=(u,v)$ is a solution of the system:
$$\begin{Bmatrix}
u^2+v^2=1\\
v=t(u+1)
\end{Bmatrix}$$
Replacing $v$ at the first equation, we get:
$$(1+t^2)u^2+2t^2u+(t^2-1)=0$$
We solve the equation and find:
$$u=\frac{1-t^2}{1+t^2} , u=-1$$
$u=-1$ corresponds to the point $A=(-1,0)$.
We calculate $v=t(u+1)=\frac{2t}{t^2+1}$, so the coordinates of $B$ are:
$$B= \left ( \frac{1-t^2}{1+t^2}, \frac{2t}{1+t^2} \right )$$
Remark:
If the slope $t \in \mathbb{Q}$, then $B=(u,v) \in \mathbb{Q} \times \mathbb{Q}$.
Conversely, if the coordinates of $B=(u,v)$ are rational, then the line $AB$ has slope $t=\frac{v-0}{u+1} \in \mathbb{Q}$.
Therefore, the set of rational solutions of $x^2+y^2=1$ is:
$$\begin{Bmatrix}
(u,v)=\left ( \frac{1-t^2}{1+t^2}, \frac{2t}{1+t^2} \right )|t \in \mathbb{Q}
\end{Bmatrix} \cup \{ (-1,0)\}$$
Remark: If $t=\frac{r}{s}, r, s \in \mathbb{Z}, (r,s)=1$, we get the Pythagorean Triples.
But... how do we get them? (Sweating)
Attachments
Last edited: