tracker890 Source h
- 90
- 11
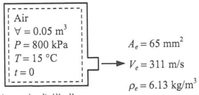
- Homework Statement
- Confusing in the conservation of mass.
- Relevant Equations
- Continuity Equation
Q: Why is air expelled from the system, yet the system's mass remains unchanged? Isn't mass related to volume?
Attachments
Last edited: