(QM) Number of states with Energy less than E

[iakmngle]

Homework Statement

Give an expression for the number of states, N , having energy less than some given E .
Assume N >> 1.

Relevant Equations

$$
\psi (x,y,z) \equiv A
\sin{\left(\frac{n_x \pi x}{a} \right)}
\sin{\left(\frac{n_y \pi y}{a} \right)}
\sin{\left(\frac{n_z \pi z}{a} \right)}
$$

Hi, so I'm having trouble with a homework problem where it asks me to find the number of states with an energy less than some given E.

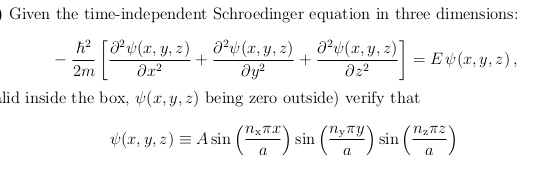
From this, I was able to work out the energy E to be
$$
E = \frac{\hbar^2}{2m} \frac{\pi^2}{a^2} \left(
n_x^2 + n_y^2 + n_z^2
\right)
$$
and also find the energy of the ground and first excited states respectively by replacing (nx,ny,nz) with (1,1,1) and (1,1,2).

I've attempted to rearrange the equation as below, but am not really sure about where to go next.
$$
n_x^2 + n_y^2 + n_z^2 = \frac{2m E a^2}{\hbar^2 \pi^2}
$$

Any guidance would be appreciated. Thanks in advance!

 

[PeroK]

I'm not sure I see any obvious way you could count up the states in this case. I have a vague recollection of looking at this once, but I can't help I'm afraid.

Is that the whole question?

 

[iakmngle]

I'm not sure I see any obvious way you could count up the states in this case. I have a vague recollection of looking at this once, but I can't help I'm afraid.

Is that the whole question?

There were a few questions leading up to this such as find the ground and first state. But the question is pretty much this.

 

[nrqed]

There were a few questions leading up to this such as find the ground and first state. But the question is pretty much this.

They say to consider the case $N \gg 1$. In that limit, the integer $n_x,n_y,n_z$ can be thought as forming a dense set, so think of them as $x,y,z$. Now, does the expression $x^2 + y^2 +z^2$ remind you of something?

 

[PeroK]

They say to consider the case $N \gg 1$. In that limit, the integer $n_x,n_y,n_z$ can be thought as forming a dense set, so think of them as $x,y,z$. Now, does the expression $x^2 + y^2 +z^2$ remind you of something?

I guess we are looking for a rough estimate rather than an expression? An expression suggests to me that we can count them precisely.

 

[iakmngle]

They say to consider the case $N \gg 1$. In that limit, the integer $n_x,n_y,n_z$ can be thought as forming a dense set, so think of them as $x,y,z$. Now, does the expression $x^2 + y^2 +z^2$ remind you of something?

That would be a sphere at the origin with a radius of $$\sqrt{\frac{2 E m a^2}{h^2 \pi^2}}$$. I'm not too sure what to do with this, could it be something with the density?

 

[PeroK]

That would be a sphere at the origin with a radius of $$\sqrt{\frac{2 E m a^2}{h^2 \pi^2}}$$. I'm not too sure what to do with this, could it be something with the density?

The idea is that if you have a state $n_x, n_y, n_z$, then you could look at that as a point in 3D space. Then it's a question of how many points lie within a given volume.