Quantitative description of successive Stern-Gerlach measurements

[Garlic]

TL;DR Summary

In an experimental setup where three Stern-Gerlach measurements were done successively, the rate at which the detector clicks was given as 25%, however my result is off by a factor of two (12,5%).
Why don't we need to take the absolute-squared of the end result to find the probability?
Does the most correct mathematical description of the Stern-Gerlach experiment involve using projection operators of spatial coordinates?

I'm trying to understand how exactly we calculate the detection rate in this specific multiple Stern-Gerlach setup.
As written on the image, an (unpolarized) atomic beam is sent through a three Stern-Gerlach apparatuses, and the detector supposedly clicks 25% of the time.

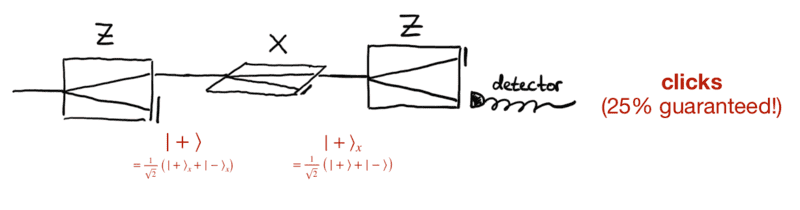
When I try to calculate the click-rate, I come across a different answer, and I am not sure if I'm wrong, or the above statement of 25% clicks are wrong.

Here is my reasoning. Could you please tell me where my mistake is? Thank you!

I make this calculation:

initial beam (unpolarized)
$$| \psi_i \rangle = \frac{1}{ \sqrt2 } ( | + \rangle + | - \rangle ) $$

after the first z-gate
$$| \psi_j \rangle = | + \rangle \langle + \psi | \psi_i \rangle = \frac{1}{ \sqrt2 } | + \rangle $$

after the x-gate:
$$ | \psi_k \rangle = | +_x \rangle \langle +_x | \psi_j \rangle = \frac{1}{2} | +_x \rangle \langle +_x | ( | +_x \rangle + | -_x \rangle ) = \frac{1}{2} | +_x \rangle $$

after the second z-gate:
$$ | \psi_l \rangle = | - \rangle \langle - | \psi_k \rangle = \frac{1}{2 \sqrt2 } | - \rangle \langle - | ( | + \rangle + | - \rangle ) = \frac{1}{2 \sqrt2} | - \rangle $$

At the detector (measurement):
$$ \langle \psi_l | \psi_l \rangle = \frac{1}{8} $$

Which would mean the detector would click 12,5% percent of the time.
(This result is only off by a factor of two, which, maybe was forgotten in the uppermost image, because they assumed an incoming beam of spin-up polarized atoms?)

However, it also confuses me that the probability to measure a state should actually be absolute-squared of the bra-ket, meaning the detector should click 1/64 of the time. I know that this result would definitely be wrong, but I don't understand WHY it is wrong.
$$| \langle \psi_l | \psi_l \rangle |^2 = \frac{1}{64} $$

Finally, it was shown to us, that the true mathematical description of the states in the Stern-Gerlach experiment, one needs to consider entangled states between the spatial (upward/downward beam) and the spin (spin up/down), such as in the picture below:

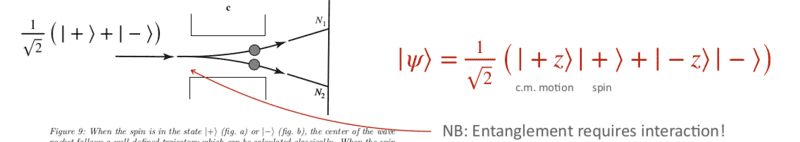
I don't understand how exactly one would make calculations using this special wave function.
$$ | \psi \rangle = \frac{1}{ \sqrt2 } ( | +z \rangle | + \rangle + | -z \rangle | - \rangle ) $$

Does the most correct mathematical description of the Stern-Gerlach experiment involve using a spatial-coordinate projector?
$$ P = | +z \rangle \langle +z | $$

 

[DrClaude]

initial beam (unpolarized)
$$| \psi_i \rangle = \frac{1}{ \sqrt2 } ( | + \rangle + | - \rangle ) $$

This is not correct. An unpolarized beam is not in a definite state, i.e., it can't be written as a ket. You have to use the density operator instead. However, this doesn't affect what you calculated after.

after the first z-gate
$$| \psi_j \rangle = | + \rangle \langle + \psi | \psi_i \rangle = \frac{1}{ \sqrt2 } | + \rangle $$

after the x-gate:
$$ | \psi_k \rangle = | +_x \rangle \langle +_x | \psi_j \rangle = \frac{1}{2} | +_x \rangle \langle +_x | ( | +_x \rangle + | -_x \rangle ) = \frac{1}{2} | +_x \rangle $$

after the second z-gate:
$$ | \psi_l \rangle = | - \rangle \langle - | \psi_k \rangle = \frac{1}{2 \sqrt2 } | - \rangle \langle - | ( | + \rangle + | - \rangle ) = \frac{1}{2 \sqrt2} | - \rangle $$

I personally do like the use of unnormalized kets, and prefer simply using probabilities of outcome after each Stern-Gerlach apparatus, with the measurement leaving the particle in a definite, normalized ket.

At the detector (measurement):
$$ \langle \psi_l | \psi_l \rangle = \frac{1}{8} $$

This is where you go wrong. This measurement is identical to those above. Project on $\bra{-}$, get $1/(2 \sqrt2)$, and get the probability as the absolute value squared, i.e., 1/8.

Which would mean the detector would click 12,5% percent of the time.
(This result is only off by a factor of two, which, maybe was forgotten in the uppermost image, because they assumed an incoming beam of spin-up polarized atoms?)

Hard to say without reading the original source. The 25% might be with respect to the output of the first SG (equivalent to state preparation).

Finally, it was shown to us, that the true mathematical description of the states in the Stern-Gerlach experiment, one needs to consider entangled states between the spatial (upward/downward beam) and the spin (spin up/down), such as in the picture below:
View attachment 337938

I don't understand how exactly one would make calculations using this special wave function.
$$ | \psi \rangle = \frac{1}{ \sqrt2 } ( | +z \rangle | + \rangle + | -z \rangle | - \rangle ) $$

Does the most correct mathematical description of the Stern-Gerlach experiment involve using a spatial-coordinate projector?
$$ P = | +z \rangle \langle +z | $$

If you want to be completely correct, you have to take into account that the spatial state is not quantized, but continuous. But this "cartoon" version is close enough for pedagogical purposes. The Projector is then indeed as you wrote it for the spatial degree of freedom, with implicitly the identity operator operating on the spin state.