- #1
pmd28
- 64
- 0
Hey all, I want to preface this with I wasn't sure if I should put this in the physics thread since it is quantum mechanics or in chemistry thread since this is for my Physical Chemistry course. I will gladly move the thread if the community feels it is more appropriate in the physics thread. I also am not aware of any equation editors as I am a returning member from a long time ago, the update is new to me.
There are three conceptual questions I attempted as practice and they are as follows:
1. Does bond length of a real molecule depend on its energy? Answer this question by referring to Figure 7.7. The bond length is the midpoint of the horizontal line connecting the two parts of V(x). (I'm assuming the two parts are split when y=0; the left and right being the separate parts)
2.The zero point energy of the particle in the box goes to zero as the length of the box approaches infinity. What is the appropriate analogue for the quantum harmonic oscillator?
3. What is the degeneracy of the energy levels for the rigid rotor in 2D? If it is not 1, explain why?My attempted solutions are the following:
1. Figure 7.7
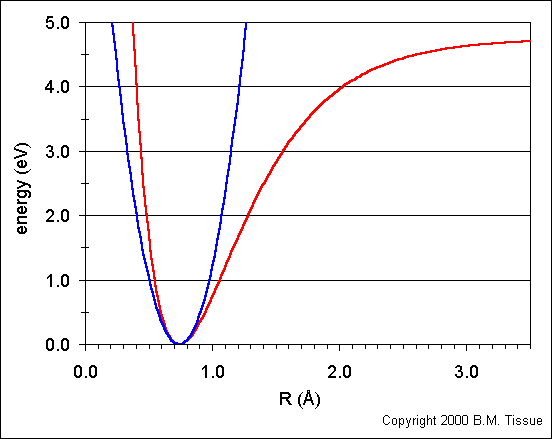
Bond length does depend on energy. As energy increases the midpoint of the horizontal moves farther to the right. (Could someone elaborate why this happens, we didn't discuss the anharmonic oscillator in too much depth during lecture)
2. En=h(n+1/2)(√k/μ). The equivalent scenario would be if k were to approach 0 or μ approach infinity. (Neither of these solutions seem very plausible physically, but I guess it's a model so we could assume hypothetical molecules which have infinitely heavy molecules or infinitely small force constants. Could some one address this?)
3. Since energies of the 2D rigid rotor are Eml=((h2)(ml2))/(2I) and ml= 0,±1,±2,... the degeneracy would be two for all ml except ml=0, in which case it would be 1. (I thought if there aren't two energetically equivalent energy levels then it's termed to have "no degeneracy").
I believe my answers are for the most part correct, but then again I'm here to double check my thought processes.
Thank You in advance.
There are three conceptual questions I attempted as practice and they are as follows:
1. Does bond length of a real molecule depend on its energy? Answer this question by referring to Figure 7.7. The bond length is the midpoint of the horizontal line connecting the two parts of V(x). (I'm assuming the two parts are split when y=0; the left and right being the separate parts)
2.The zero point energy of the particle in the box goes to zero as the length of the box approaches infinity. What is the appropriate analogue for the quantum harmonic oscillator?
3. What is the degeneracy of the energy levels for the rigid rotor in 2D? If it is not 1, explain why?My attempted solutions are the following:
1. Figure 7.7
Bond length does depend on energy. As energy increases the midpoint of the horizontal moves farther to the right. (Could someone elaborate why this happens, we didn't discuss the anharmonic oscillator in too much depth during lecture)
2. En=
3. Since energies of the 2D rigid rotor are Eml=((
I believe my answers are for the most part correct, but then again I'm here to double check my thought processes.
Thank You in advance.