Quantum Hall Effect resistivity

[rwooduk]

I'm having trouble understanding why the resistivity behaves as it does in comparison to the density of states for the quantum hall effect. Take the following two diagrams:
(A)

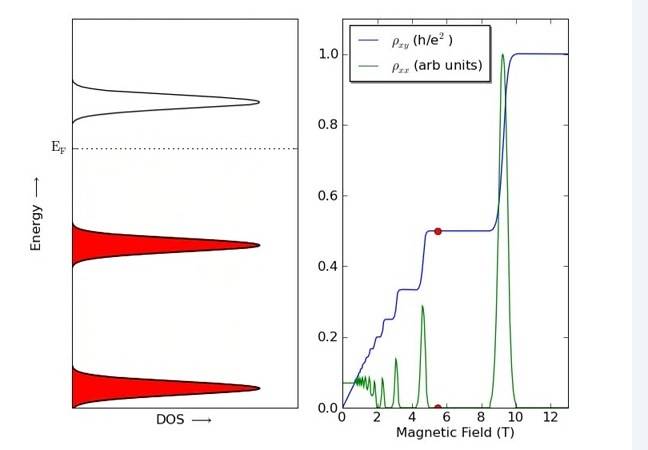
(B)

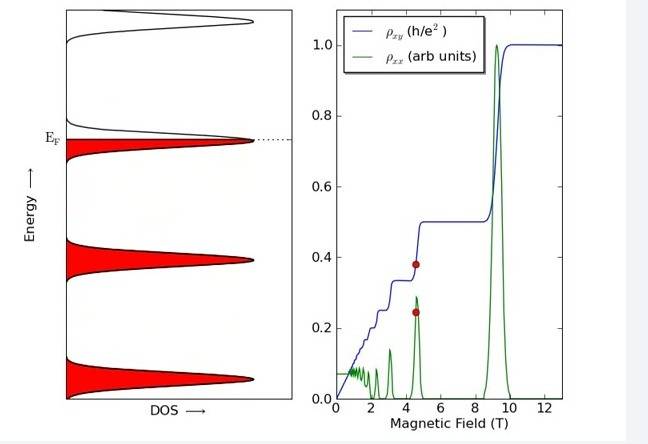
I understand that there can be no scattering in (A) because all states are full (i.e. no elastic) and the gap is too big to scatter inelastically. But why should the resistivity remain constant?

Also on (B) why does the resistivity increase when there are free states to scatter into? Is it saying scattering hinders conduction?

Having real trouble relating the DOS to resistivity. Any suggestions more than welcome.

 

[rwooduk]

Ok, I'll update this. Since there are more free states in (b) the scattering increases and so does the resistivity.

For (A) when there are no states available it drops to zero.

^^ This is for the XY component. I'm still a little unsure of the difference (aside from direction) of the XX and XY plots. So any advice would be appreciated.

 

[radium]

There is no back scattering because the edge states are chiral, the direction is determined by the B field. The diagonal components of the conductivity matrix (when you have the chemical potential between bands) are zero because there is no current along the direction of the electric field except when the gap closes. When this happens the system becomes a metal, both the conductivity and resistivity are then nonzero. The resistivity is the inverse of conductivity, there can be no resistivity for this reason, the inverse of conductivity is not diagonal it is off diagonal. When the gap closes there is a phase transition between an insulator with hall conductivity ne^2/h and (n+1)e^2/h. When there are impurities there is still no backscattering of the edge states, they will just go around the impurity. There can't be backscattering, the states are chiral.

The quantization of the hall conductance is not for the sigma xx it is only for sigma xy. If there is a gap, the system is an insulator, there can't be a current in the bulk (xx direction).

 

[rwooduk]

There is no back scattering because the edge states are chiral, the direction is determined by the B field. The diagonal components of the conductivity matrix (when you have the chemical potential between bands) are zero because there is no current along the direction of the electric field except when the gap closes. When this happens the system becomes a metal, both the conductivity and resistivity are then nonzero. The resistivity is the inverse of conductivity, there can be no resistivity for this reason, the inverse of conductivity is not diagonal it is off diagonal. When the gap closes there is a phase transition between an insulator with hall conductivity ne^2/h and (n+1)e^2/h. When there are impurities there is still no backscattering of the edge states, they will just go around the impurity. There can't be backscattering, the states are chiral.

The quantization of the hall conductance is not for the sigma xx it is only for sigma xy. If there is a gap, the system is an insulator, there can't be a current in the bulk (xx direction).

Thats very helpful! Thank you!