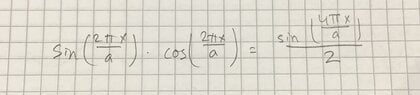Quantum mechanics - infinite square well problem

[Graham87]

Homework Statement

For a wave function evaluate the following integral

Relevant Equations

Infinite square well equations

I have solved c), but don’t know how to solve the integral in d.
It looks like an integral to get c_n (photo below), but I still can’t figure out what to make of c) in the integral of d).

I also thought maybe you can rewrite c) into an initial wave function (photo below) with A,x,a but don’t know how.

Thanks!

 

[TSny]

I have solved c), but don’t know how to solve the integral in d.

Consider using a trig identity to write $\sin\left(\frac{2\pi}{a}x\right)\cos\left(\frac{2\pi}{a}x\right)$ in a way that will be helpful in evaluating the integral.

 

[Graham87]

I tried like this already, but I still don’t know how to deal with c) in the integral.

 

[TSny]

I tried like this already, but I still don’t know how to deal with c) in the integral.

OK, good. Can you relate $\large\frac{\sin\left(\frac{4\pi x}{a}\right)}{2}$ to one of the $\psi_n(x)$?

 

[Graham87]

OK, good. Can you relate $\large\frac{\sin\left(\frac{4\pi x}{a}\right)}{2}$ to one of the $\psi_n(x)$?

ψ4(x) ?

 

[TSny]

ψ4(x) ?

Exactly what is the relation between $\large\frac{\sin\left(\frac{4\pi x}{a}\right)}{2}$ and $\psi_4(x)$?

 

[Graham87]

Exactly what is the relation between $\large\frac{\sin\left(\frac{4\pi x}{a}\right)}{2}$ and $\psi_4(x)$?

Same n?
How does this look?

I don’t think it’s correct because c_4 is not the same answer.

 

[TSny]

How does this look?View attachment 303556

That will work.

However, it's maybe a little nicer to show $\large\frac{\sin\left(\frac{4\pi x}{a}\right)}{2} = \frac{\sqrt{2a}}{4}\psi_4(x)$ . Then you don't need to do any explicit integration. Just use the orthonormality of the $\psi_n(x)$.

 

[Graham87]

That will work.

However, it's maybe a little nicer to show $\large\frac{\sin\left(\frac{4\pi x}{a}\right)}{2} = \frac{\sqrt{2a}}{4}\psi_4(x)$ . Then you don't need to do any explicit integration. Just use the orthonormality of the $\psi_n(x)$.

So like this?

I found the integral d) similar to this.

Is it wrong to assume that c_4 should be the same as my answer in d)?
In that case my answer in d is not correct.

 

[vela]

You're asking, are
$$\frac{\sqrt{2a}}{4} \int \psi_4^2\,dx$$ and $$\int \psi_4^2\,dx$$ equal? I think you should be able to answer that on your own. :)

 

[TSny]

You need to calculate $\int_0^a{\sin\left(\frac{2\pi x}{a}\right)\cos\left(\frac{2\pi x}{a}\right)}\Psi(x,0)dx$

Write this as $\frac{\sqrt{2a}}{4}\int_0^a\psi_4(x)\Psi(x,0)dx$.

Substitute the given expression for $\Psi(x,0)$ and evaluate using the orthonormality of the $\psi_n(x)$.

You should get the same answer as you got in post #7.

 

[Graham87]

Big thanks! Got it!

 

[PeroK]

Big thanks! Got it!

In general, it's a good habit to use the notation $\psi_n(x)$ and use the general properties of eigenfunctions - especially orthonormality - as much as possible. And only resort to the specific eigenfunctions when necessary.