- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Quantum version of Larmor precession
- Thread starter Bobs
- Start date
In summary, there is a conversation about a problem involving a quantum system evolving under different magnetic fields. The initial state of the system is given and the problem involves finding the probability of the system being in a certain state at a certain time. There is some confusion about the correct way to approach the problem and different answers are being proposed. The correct probability is still being determined.
Physics news on Phys.org
- #2
TSny
Science Advisor
Homework Helper
Gold Member
2023 Award
- 14,582
- 4,639
Hello. I haven't gone through all of the details of your calculations. But, I don't see where you have taken into account the evolution of the system between ##t = 0## and ##t = T##. It appears to me that you are assuming that the system is in state ##\chi_+^{(x)}## at time ##t = T##.
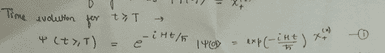
Attachments
- #3
Bobs
- 14
- 1
Do you see any mistakes at the final answer? And yes, I'm assuming that the system in state ##\chi_+^{(x)}## at time ##t=T##. Staying tuned for your sincerely reply!
- #4
TSny
Science Advisor
Homework Helper
Gold Member
2023 Award
- 14,582
- 4,639
Maybe we are interpreting the statement of the problem differently. The way I read it, at time ##t = 0## the system is in state ##|\psi(0) \rangle = \chi_+^{(x)}##. It evolves for time ##T## with ##\mathbf B## in the z direction. Then, in the time interval ##T \leq t \leq 2T## it evolves with ##\mathbf B## in the y direction. So, you will need to find ##|\psi(T) \rangle## before you can determine the state for ##t > T##.
Your final result for the probability appears to be a complex number. But probabilities are real numbers. Also, shouldn't the answer depend on the magnetic field strength B?
Your final result for the probability appears to be a complex number. But probabilities are real numbers. Also, shouldn't the answer depend on the magnetic field strength B?
- #5
Chandra Prayaga
Science Advisor
- 652
- 150
It looks like this post has appeared twice.
The systaem will not be in state ##\chi_+^{(x)}## at t = T. As TSny points out in the above post, the evolution between t = 0 and t = T is dictated by the magnetic field only in the z direction. You should calculate |ψ(T)> from that, and then let that evolve from t = T to t = 2T with the magnetic field only in the y direction.Bobs said:Do you see any mistakes at the final answer? And yes, I'm assuming that the system in state at time ##t=T##. Staying tuned for your sincerely reply!
- #6
Bobs
- 14
- 1
I found the probability as ##\dfrac{B^2}{2}## is that correct?
- #7
vela
Staff Emeritus
Science Advisor
Homework Helper
Education Advisor
- 16,090
- 2,732
That answer can't possibly be correct. Probabilities are unitless.Bobs said:I found the probability as ##\dfrac{B^2}{2}## is that correct?
- #8
Bobs
- 14
- 1
Finally, I've found the probability as ##0## from ##P = \dfrac{1}{4}exp \biggr( \dfrac{-2t\mu BB}{\hbar}\biggr ) \biggr | (1-1) \biggr |^2 = 0## Does that seem correct now? Thanks in advance.
- #9
Chandra Prayaga
Science Advisor
- 652
- 150
What steps did you follow to arrive at that answer?
- #10
Bobs
- 14
- 1
Is that correct? Or what would be the correct probability we're looking for? I'm receiving too many different answers.
- #11
vela
Staff Emeritus
Science Advisor
Homework Helper
Education Advisor
- 16,090
- 2,732
No. The argument of the exponential should be unitless.
FAQ: Quantum version of Larmor precession
What is the "quantum version" of Larmor precession?
The quantum version of Larmor precession is a phenomenon that occurs when a quantum system with a magnetic moment is placed in a magnetic field. It describes the precession, or spinning, of the system's magnetic moment around the direction of the magnetic field.
How does the quantum version of Larmor precession differ from the classical version?
In the classical version of Larmor precession, the magnetic moment can have any orientation with respect to the magnetic field. However, in the quantum version, the magnetic moment can only be aligned in one of a few discrete orientations, determined by the quantum properties of the system.
What is the significance of Larmor precession in quantum systems?
Larmor precession is important in quantum systems because it provides a way to measure the magnetic properties of these systems. By observing the precession of the magnetic moment, researchers can gain insight into the quantum properties of the system.
Can the quantum version of Larmor precession be observed in everyday life?
No, the quantum version of Larmor precession is a phenomenon that occurs at the scale of individual atoms and subatomic particles. It cannot be observed in everyday life, but it is an important concept in quantum physics and has practical applications in fields such as magnetic resonance imaging (MRI).
How is the quantum version of Larmor precession used in modern technology?
The quantum version of Larmor precession is used in technologies such as MRI and nuclear magnetic resonance (NMR) spectroscopy. In these applications, the precession of the magnetic moment is used to create detailed images or to analyze the chemical composition of a substance.
Similar threads
- Replies
- 1
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 3
- Views
- 1K
- Replies
- 6
- Views
- 4K
- Replies
- 2
- Views
- 2K
- Replies
- 6
- Views
- 2K
- Replies
- 1
- Views
- 2K
- Replies
- 1
- Views
- 2K
- Replies
- 4
- Views
- 2K
- Replies
- 1
- Views
- 2K
Share:

