Query regarding Fermi Gas model

[Saptarshi Sarkar]

TL;DR Summary

What is the reason behind the exponential part of the well of a proton in the fermi gas model

I was reading an introductory text on nuclear models and came across the Fermi Gas model. I understand that the depth of the potential well of the proton should be less than the depth of the potential well of the neutron due to the Coulombic repulsion between the protons.

But I did not understand the reason behind the red part of the potential in the following diagram.

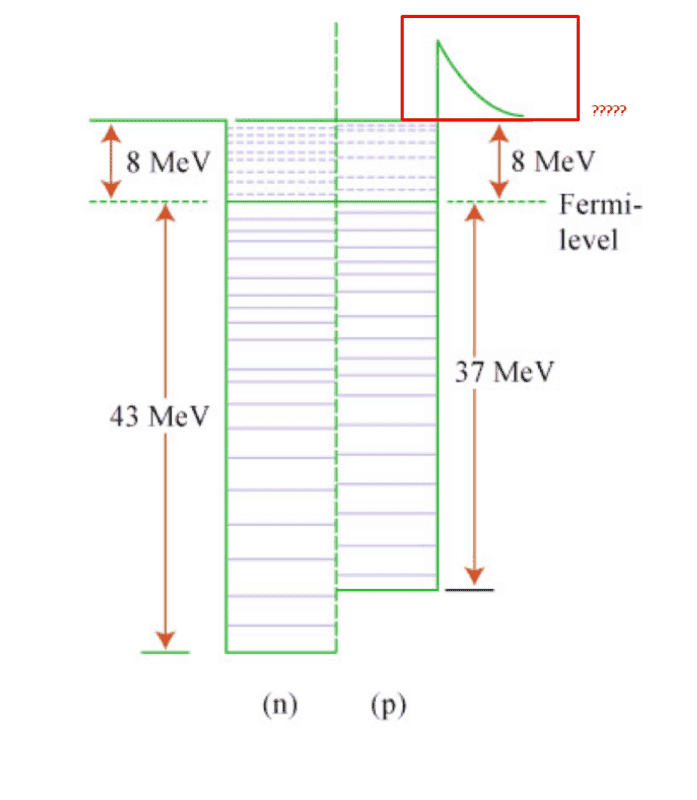
To me, it looks like the red part shows that it is more difficult to pull out a proton from the nucleus that a neutron. But that shouldn't be true as the Coulombic repulsion should make it easier.

 

[Orodruin]

You are missing that the bottom of the proton potential is higher.

What is important is the height from the bottom to the top. Classically this is the barrier you would need to overcome. Quantum mechanically, the proton can tunnel out through the Coulomb barrier already at lower energies than the top of the potential.

 

[Orodruin]

Summary:: What is the reason behind the exponential part of the well of a proton in the fermi gas model

Also, it is not exponential, it is the Coulomb potential outside the nucleus where the potential due to the strong nuclear force is zero.

 

[Saptarshi Sarkar]

You are missing that the bottom of the proton potential is higher.

What is important is the height from the bottom to the top. Classically this is the barrier you would need to overcome. Quantum mechanically, the proton can tunnel out through the Coulomb barrier already at lower energies than the top of the potential.

Shouldn't the barrier be less deep due to the Coulomb repulsion between the protons in the nucleus? Why then should it be raised above?

I am unable to understand why the proton needs higher energy to leave the nucleus than the neutron. They both are under the same nuclear attractive force but the proton has a repulsive force too. Shouldn't it be easier to remove a proton than a neutron?

Why does a proton need to Quantum tunnel to leave the well? Which potential is preventing it from leaving?

 

[Orodruin]

Shouldn't the barrier be less deep due to the Coulomb repulsion between the protons in the nucleus? Why then should it be raised above?

No. The potential is the superposition of the strong and the Coulomb potential. The ”height” from the bottom to the top is due to the stronh potential, which is the same for both. The Coulomb potential is continuous. In comparison to the value at infinity, the depth is smaller due to Coulomb repulsion as is clearly seen in the image.

I suggest that you think about the neutron potential (which is only strong) and then ask yourself what happens when you add a repulsive Coulomb potential to it.

Why does a proton need to Quantum tunnel to leave the well? Which potential is preventing it from leaving?

Because there is a potential barrier due to the Coulomb potential. Note that neutrons with less than the classical energy needed to escape cannot escape in the quantum case either.

 

[vanhees71]

You are missing that the bottom of the proton potential is higher.

What is important is the height from the bottom to the top. Classically this is the barrier you would need to overcome. Quantum mechanically, the proton can tunnel out through the Coulomb barrier already at lower energies than the top of the potential.

It's not so much the proton that tunnels but $^4\text{He}$ nuclei, aka $\alpha$ particles (look for Gamow model of $\alpha$ decay in any good nuclear-physics textbook).

Of course also the "box potential" for the strong-interaction part is a very simplified effective description. In fact the nuclear many-body problem is a very complicated issue. The nucleon-nucleon interaction is not a simple two-body interaction but needs multi-body interactions. A modern approach is effective chiral symmetry and renormalization-group approaches to describe this complicated many-body problem.

 

[Saptarshi Sarkar]

It's not so much the proton that tunnels but $^4\text{He}$ nuclei, aka $\alpha$ particles (look for Gamow model of $\alpha$ decay in any good nuclear-physics textbook).

I am having trouble understanding why any positivity charged particle like the proton or the alpha particle should have a coulomb barrier which prevents it from leaving directly. Only the nuclear force can do that . There is no negetive charges inside the nucleus that is trying to keep it inside the nucleus.

 

[vanhees71]

But your picture in #1 nicely shows that. The right potential pot is for the protons. It models the strong-interaction part of a single proton within the nucleus by
$$V_{\text{strong}}=-V_0 \Theta(R-r_0).$$
The Coulomb potential outside of this box is of course given by
$$V_{\text{Coulomb}}=\frac{(Z-1) e^2}{4 \pi r} \Theta(r_0-R).$$

 

[Dr_Nate]

I think you need to compare apples to apples. Count up the same number of energy levels in each nucleon's well and look at the energy difference. For example, you could use the first level. The proton in the first level is at a higher energy than a neutron at the first level. This shifted energy is going to be the extra energy that gives a greater chance to tunnel out (of course the topmost nucleons are the ones that are more likely to tunnel out).

 

[Saptarshi Sarkar]

I read about the tunnel theory of alpha decay in the book by Arthur Beiser. Here are a few lines from the book.

"Here is a plot of the potential energy U of an alpha particle as a function of its distance r from the center of a certain heavy nucleus. The height of the potential barrier is about 25 MeV, which is equal to the work that must be done against the repulsive electric force to bring an alpha particle from infinity to a position adjacent to the nucleus but just outside the range of it's attractive forces. We may therefore regard an alpha particle in such a nucleus as being inside a box whose walls require an energy of 25 MeV to be surmounted"

Now, the thing that I am unable to understand is why is the alpha particle required to have 25 MeV (classically) energy to leave the nucleus.

I understand that that amount of energy is required to bring it towards the nucleus as the force is repulsive, but to move away from the nucleus, it should already be able to do it with the help of the repulsive forces.

In my mind I imagined the alpha particle to be a ball that I kept on a shelf, to put it on the shelf I need to do work in opposing the gravitational force. But if it's already on the shelf, shouldn't it be easily able to fall down ?

 

[Dr_Nate]

It's not so much the proton that tunnels but $^4\text{He}$ nuclei, aka $\alpha$ particles (look for Gamow model of $\alpha$ decay in any good nuclear-physics textbook).

This is not my field, but I don't think alpha decay is a general method for nucleons to tunnel out. The isotopes that we encounter on earth, yes, have alpha decay as the dominant way that nucleons tunnel out. However, we see other dominant decay mechanisms in more unstable isotopes.

 

[Dr_Nate]

Now, the thing that I am unable to understand is why is the alpha particle required to have 25 MeV (classically) energy to leave the nucleus.

Thinking classically in a quantum mechanical problem is usually not the way to go. That being said: classically, the only way any of us can be unbound from Earth's gravitational well is to be at the escape velocity at Earth's surface. We need the kinetic energy.

I understand that that amount of energy is required to bring it towards the nucleus as the force is repulsive, but to move away from the nucleus, it should already be able to do it with the help of the repulsive forces.

Well, you still need to conserve energy. The potential and kinetic energies of the particles after still need to sum to the energies before.

 

[vanhees71]

This is not my field, but I don't think alpha decay is a general method for nucleons to tunnel out. The isotopes that we encounter on earth, yes, have alpha decay as the dominant way that nucleons tunnel out. However, we see other dominant decay mechanisms in more unstable isotopes.

Sure, there are many more decay mechanisms, but concerning the tunnel effect $\alpha$ decay is the prime textbook example for a real-world application (Gamow theory of $\alpha$ decay).

 

[Orodruin]

I understand that that amount of energy is required to bring it towards the nucleus as the force is repulsive, but to move away from the nucleus, it should already be able to do it with the help of the repulsive forces.

If you look at the potential of the strong nuclear interaction, that is what gives you an attractive force. The contribution from the electrostatic force is always repulsive. However, the potential barrier is the combination of the two - not only Coulomb potential.

 

[vanhees71]

I must admit, I never understood, why it's often called the "Coulomb barrier" though it's not a barrier but repulsive. Of course, it's the total potential strong+em. which leads to bound states (a repulsive Coulomb potential of course has no bound states at all), and that's why you have a tunneling effect here, i.e., the fact that there's some probability to find the particle with a determined energy $E$ in regions where the particle within the classical description cannot be for reasons of energy conservation.