Question about a double integral region

[Amaelle]

Homework Statement

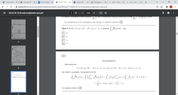
look at the image

Relevant Equations

double integral

Greetings All!

I have a problem finding the correct solution at first glance

My error was to determine the region of integration , for doing so I had to the intersection between y= sqrt(x) and y=2-x

to do so
x=(2-x)^2
to find at the end that x=1 or x=5

while graphically we can see that the region start from x=0 they intersect in x=1 and never meet again!

could someone help me with my confusion ?

Thank you!

√

 

[anuttarasammyak]

Drawing the region on xy plane would help you.

 

[Amaelle]

Drawing the region on xy plane would help you.

yes this i what I done
I just want to know why my analitical results was wrong

 

[fresh_42]

Where exactly was your confusion? The region looks like this:
https://www.wolframalpha.com/input?i=root(x)+<+y+<+2-x
$x$ is in $[0,1]$ and $y$ in $[0,\sqrt{2}]$.

I don't see where you got $x=5$ from. Say $t:=\sqrt{x}$. Then $t^2+t-2=\left(t+1/2\right)^2-(1.5)^2\leq 0$ and so $0\leq t = \sqrt{x} \leq 1.5-0.5=1$.

 

[Delta2]

The solutions are x=1 and x=4 but the x=4 solution is not accepted because we want 2-x to be greater than zero. Remember that the inequality is $$0\leq \sqrt x\leq y\leq 2-x$$

 

[Amaelle]

The solutions are x=1 and x=4 but the x=4 solution is not accepted because we want 2-x to be greater than zero. Remember that the inequality is $$0\leq \sqrt x\leq y\leq 2-x$$

thanks a million! you nail it!