FranzDiCoccio
- 350
- 43
Summary:: I've found an exercise about sparks caused by back emf. The exercise is based on a mathematical model of the current flowing in the circuit around the time when the switch is closed.
I'm wondering to what extend that model is realistic
The exercise I'm referring to proposes this function for the current
<br /> i(t) = \left\{<br /> \begin{array}{ll}<br /> \displaystyle\frac{t^2+a t + b}{(t-4)^2} & 0\leq t \leq 3 \\<br /> e^{-c(t-3)} & t>3<br /> \end{array}<br /> \right.<br />
where the parameters are such that the graph of the function is
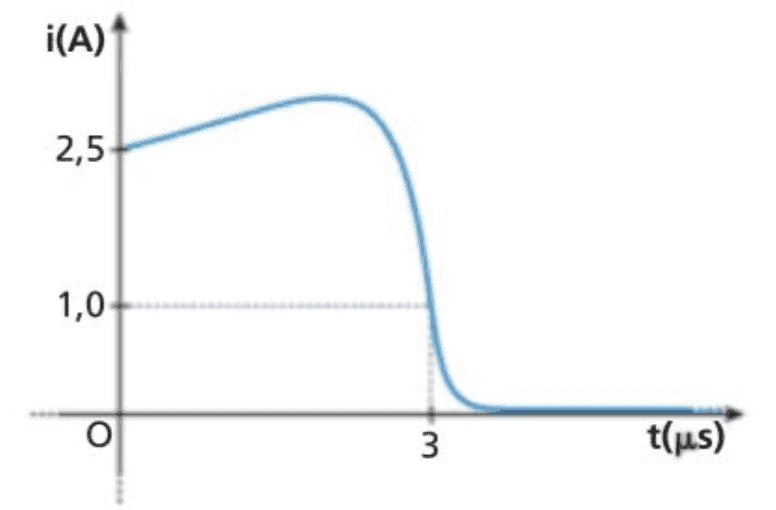
Then the problem gives the self-inductance of the circuit and the breakdown voltage, and asks for the time at which the spark happens.
The problem is not too hard, per se.
I'm wondering: is the given function any realistic? If so, is there any simple argument that explains why?
The only thing I can think of is that the given function is a smoothed out "heuristic" version of the two functions describing the charging and the discharging of an inductor. The first part grows as ## i_{\rm max} (1-e^{-t/\tau})##, the second decreases as ## i_{\rm max} e^{-t/\tau}##.
The other possibility is that the given function is not realistic and was devised for the only purpose of making this exercise solvable.
Thanks a lot for any insight
I'm wondering to what extend that model is realistic
The exercise I'm referring to proposes this function for the current
<br /> i(t) = \left\{<br /> \begin{array}{ll}<br /> \displaystyle\frac{t^2+a t + b}{(t-4)^2} & 0\leq t \leq 3 \\<br /> e^{-c(t-3)} & t>3<br /> \end{array}<br /> \right.<br />
where the parameters are such that the graph of the function is
Then the problem gives the self-inductance of the circuit and the breakdown voltage, and asks for the time at which the spark happens.
The problem is not too hard, per se.
I'm wondering: is the given function any realistic? If so, is there any simple argument that explains why?
The only thing I can think of is that the given function is a smoothed out "heuristic" version of the two functions describing the charging and the discharging of an inductor. The first part grows as ## i_{\rm max} (1-e^{-t/\tau})##, the second decreases as ## i_{\rm max} e^{-t/\tau}##.
The other possibility is that the given function is not realistic and was devised for the only purpose of making this exercise solvable.
Thanks a lot for any insight