Explaining a Stronger Relativity Paradox than the Twin Paradox

[kvdr]

TL;DR Summary

Question about stronger relativity paradox than twin paradox.

The twin paradox can be explained by changing reference frames. But I’m really curious how this paradox can be explained.
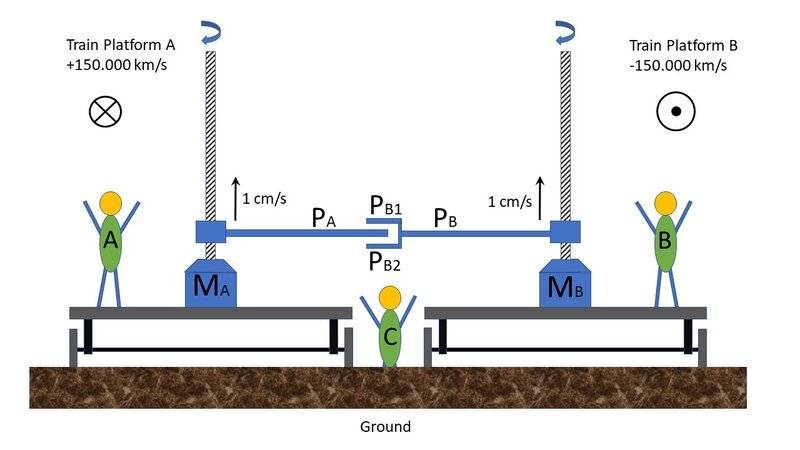
In the situation below there are three observers:

• A: Standing at a moving train platform moving at a speed of c/2 relative to “the ground”.
• B: Standing at a moving train platform moving at a speed of c/2 relative to “the ground”, but in the opposite direction as A.
• C: Does not move against the ground.

On train platform A and B there are long plates (PA, PB) that both move upwards with a speed of 1cm/s.
So, what does every observer see:

• C: A and B move at the same speed (in opposite directions) relative to C, so plate PA stays between PB1 and PB2. => nothing breaks
• A: sees that B moves at high speed. According the relativity theory everything on platform B is going slower. So, the upward speed of plate PB (1 cm/s) will also be lower. Therefore, plate PA will bump against plate PB1. => plate PB1 breaks
• B: sees that A moves at high speed. According the relativity theory everything on platform A is going slower. So, the upward speed of plate PA (1 cm/s) will also be lower. Therefore, plate PB2 will bump against plate PA. => plate PB2 breaks

So, the three observers arrive in a completely different reality. (C: nothing breaks, A: PB1 breaks, B: PB2 breaks)
Can someone please explain what really happens and how that is in accordance with relativity theory.
Thank you!

 

[Halc]

You're showing end-view, so the dimensions of the 'plate' along the direction of motion is unspecified, but I presume this means that they're not just rods passing at a single moment without collision.

The plates moving upward require each end to be raised in sync, which requires a clock synced to one frame (presumably the frame of the moving platform) and not the others. Since the clocks will not read the same time as they pass each other, the plates will collide and things will 'break' as you put it.

Where are the observers? At the front of the plates, middle, or end? They'll only be in each other's presence momentarily, so they're not expected to observe the same local thing. Assuming they're at the front and things look like the picture at the beginning, both observers A and B will each see the front of his own horizontal plate get hit by the contracted and angled far plate which locally rises faster due to its non-horizontal orientation. So none of your answers describe that.

Observer C sees the same collisions occur, but not right in front of him.

 

[PeterDonis]

The twin paradox can be explained by changing reference frames.

No, it can't. Changing reference frames can't explain anything, since any actual physics is independent of any choice of reference frames.

 

[PeterDonis]

On train platform A and B there are long plates (PA, PB) that both move upwards with a speed of 1cm/s.

There is no way to even set up this scenario, because of relativity of simultaneity. If all parts of PA are at the same height at the same time relative to A, they won't be relative to B; and if all parts of PB are at the same height at the same time relative to B, they won't be relative to A. So the plates can't even be set up as you describe.

 

[PAllen]

I think the implication is that the set up pictured is achieved in C reference frame. And that the plates themselves and the 1 cm/sec motion are all perpendicular to the relative motions of A and B with respect to C (A and B are moving toward 'you' and away from 'you' as you view the picture). Then it will look different (and symmetric) for A and B. And if there is no collision per C, there obviously won't be per A or B.

 

[PeterDonis]

I think the implication is that the set up pictured is achieved in C reference frame.

If that is the case, then PA and PB will not all be at the same height at the same time according to either A or B. I doubt that is what the OP intended, although, as you note, it is actually doable and results in no collision.

 

[PAllen]

If that is the case, then PA and PB will not all be at the same height at the same time according to either A or B. I doubt that is what the OP intended, although, as you note, it is actually doable and results in no collision.

My guess remains that is what was intended, but the OP had no idea of how different things would appear for A or B. In particular, no knowledge that both plates would be slanted per A or B by virtue of relativity of simultaneity, and that this can avoid the collision.

 

[A.T.]

According the relativity theory everything on platform B is going slower. ...

That is just one aspect of the Lorentz transformation. You have to apply the full transformation like shown here:



As you see at 2:00 the long object can have different orientation in different frames. The same will be true for the connection between the trains moving upwards, if you make frame transformations along the out-of-image dimension. Your current diagram doesn't even show the key dimension along which you make frame transformations.

 

[Ibix]

As others have noted, this experiment depends on the relativity of simultaneity which you have not accounted for in your description. Essentially, the plates turn out to remain horizontal in at most one of the frames. If you've rigged things so that they are both horizontal in the same frame (non-trivial because that would require that at least one plate is sloped in its rest frame and different points on the plates don't start rising at the same time) then everyone will agree that the plates always mesh, because the differing lift rates, slopes, and start times will combine with the horizontal motion of the platforms and always lead to the plates meshing. If you haven't rigged it like that then the plates won't mesh at all in any frame.

 

[kvdr]

To make the experiment clearer I offer some extra information.

The picture below gives a view from above.

• The train and plates are very long (infinite).
• On each platform we set an observer (A, B), and also on regular places on the ground (C).
• In the begin situation:
  • the trains do not move.
  • the plates move already at constant speed (1cm/s)
  • PA is in between PB1 and PB2.
• The trains accelerate symmetrically till they reach their final speed: +/-150.000km/s
• The engines (MA, MB) that lift the plates can be considered as clocks. (position => time)

Note that all observers of type

• A: see plate PA will bump against plate PB1. => plate PB1 breaks.
• B: see plate PB2 will bump against plate PA. => plate PB2 breaks.
• C: see plate PA stays between PB1 and PB2. => nothing breaks

 

[Ibix]

Note that all observers of type

• A: see plate PA will bump against plate PB1. => plate PB1 breaks.
• B: see plate PB2 will bump against plate PA. => plate PB2 breaks.
• C: see plate PA stays between PB1 and PB2. => nothing breaks

No, because you have still failed to account for the relativity of simultaneity, and have just made the problem more complex by introducing acceleration. A problem you could do with pen and paper is one where the carts are always moving at constant speed. You just need to specify the frame in which the plates are horizontal (probably C's (edit: has to be C's if the lifting devices are identical, in fact)) and work from there. You also need to use the full Lorentz transforms rather than just time dilation, which is a special case of the Lorentz transforms that isn't sufficient for this problem where you have synchronisation issues.

There is no paradox in the accelerating case either, by the way, but it's vastly more complex and offers no additional insight.

 

[kvdr]

There is no paradox in the accelerating case either

Then it shouldn’t be a problem to answer the question what will happen in this example.

but it's vastly more complex and offers no additional insight.

This is the way to say that you cannot solve the paradox. Prove that I’m wrong! You even don’t have to give any formula or calculate anything, just give an explanation that makes any sense.

A problem you could do with pen and paper is one where the carts are always moving at constant speed.

No problem for me to keep it simple. Go ahead!

You just need to specify the frame in which the plates are horizontal

Now I worry a bit that you did not understand the question. In my opinion all plates are all the time horizontal to all observers (A, B, C). (Unless you refer to a very minor issue, but that is applicable for the 3 observers.)

(probably C's (edit: has to be C's if the lifting devices are identical, in fact)) and work from there.

C is the easy one. Without any calculation I can tell you that for this observer plate PA always stays between PB1 and PB2, because the trains move in a 100% symmetrical way for C. => nothing breaks

Now the challenge for you is to choose observer A or B, and explain what happens so that this observer does not see plates bumping against each other.

Good luck!

 

[Ibix]

Now I worry a bit that you did not understand the question. In my opinion all plates are all the time horizontal to all observers (A, B, C).

I understand the question perfectly - but you don't appear to do so. The rising plates cannot be horizontal in more than one frame due to the relativity of simultaneity, which you seem to be completely oblivious to despite several comments already pointing it out.

Here's a side elevation of the situation, as drawn using C's rest frame. The carts move with equal and opposite velocities, green to the right and red to the left in keeping with maritime customs. The plates are horizontal and have risen by the same amount during the cross over.

Now let's sketch it in the rest frame of the red cart. The green cart is still moving to the right, but faster, and the red cart is, of course, stationary. The plates are slanted. I've added fine black horizontal and vertical lines linking the green and red carts before and after so you can see that the red cart's platform has risen further than the green cart's during the cross over. The platforms remain aligned due to the slant and the motion of the green cart, so there is no collision.

These diagrams are not to scale, but the concepts are there.

Now the challenge for you is to choose observer A or B, and explain what happens so that this observer does not see plates bumping against each other.

I already know how to resolve this. I've also already told you how your analysis fails - you are using a special case of the Lorentz transforms in a situation for which it is not appropriate. There's no point in me doing the full analysis - you're the one who needs to learn how to use simple relativistic tools if you want to think about this stuff.

You need to write down the $x$, $y$, and $t$ coordinates of the ends of the plates at the beginning and end of the cross over (or a general expression for the location of the surface of contact) and transform it. Then you need to look up the Lorentz transforms and transform the coordinates into the primed frame and see what that means in terms of how the platforms are shaped in this frame. You already have a qualitative picture of the answer from my diagrams. Post your working if you get stuck. (You may wish to read the LaTeX Guide linked below the reply box in order to post readable maths.)

 

[PAllen]

Now I worry a bit that you did not understand the question. In my opinion all plates are all the time horizontal to all observers (A, B, C). (Unless you refer to a very minor issue, but that is applicable for the 3 observers.)

No, this is flat out wrong, as has been explained several times in this thread. Because of relativity of simultaneity, which you have completely ignored and show no sign of understanding, if the plates are horizontal in frame C, they will not be horizontal in frames A or B.

 

[PeterDonis]

In my opinion all plates are all the time horizontal to all observers (A, B, C).

This is not correct, as has been repeatedly pointed out. If you are unwilling or unable to understand this, there is no point in further discussion.

 

[PeterDonis]

Now the challenge for you is to choose observer A or B, and explain what happens so that this observer does not see plates bumping against each other.

Good luck!

The only challenge here is for you, to understand why the plates are not horizontal for A and B if they are horizontal for C. You have been given more than enough information for this. Good luck.

Thread closed.