- #1
mopit_011
- 17
- 8
- Homework Statement
- At time t = 0, a small ball is released on the track shown, with an initial rightward velocity. Assume the ball always rolls along the track without slipping.
- Relevant Equations
- N/A
(This is the diagram from the problem.)
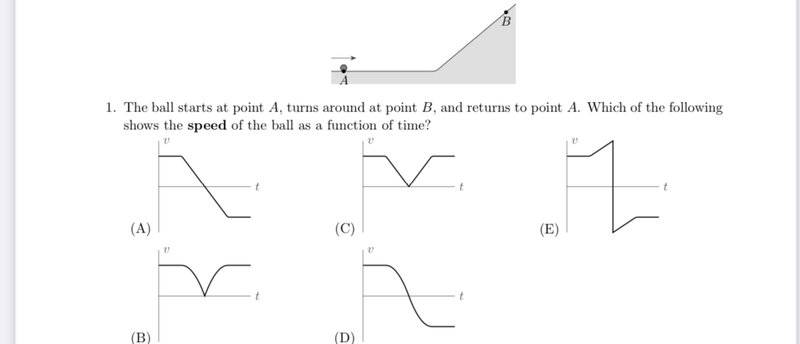
My professor assigned this as extra practice and I don’t understand why the answer is (C) instead of (B). Why would sharp bends be the correct answer? Isn’t the curved diagram more accurate for movement on a slope?
My professor assigned this as extra practice and I don’t understand why the answer is (C) instead of (B). Why would sharp bends be the correct answer? Isn’t the curved diagram more accurate for movement on a slope?