Question about Euclid's parallel postulate (5th postulate).

[parshyaa]

Why can't we prove euclids fifth postulate
What's wrong in this proof:

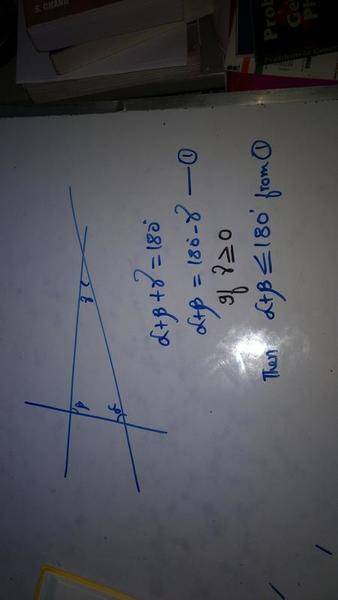
why can't we prove that there is only one line which passes through a single point which is parallel to a line.
If we can prove that two lines are parallel by proving that the alternate angles of a transverse passing through parallel side must be equal.

Then we could show that when a line throught that point behaves same then it will be parallel.

I know that euclids 5th postulate is unproveable and thus we have non-euclidean geometry, but i want to know what's wrong in my proof.

 

[phyzguy]

The external angle theorem, as you have stated it, is only provable if we assume the parallel postulate to be true. So your proposed proof of the parallel postulate is circular.

 

[parshyaa]

The external angle theorem, as you have stated it, is only provable if we assume the parallel postulate to be true. So your proposed proof of the parallel postulate is circular.

How?
Tell me Where did i used parallel postulate to prove exterior angle theorem.

 

[Svein]

Tell me Where did i used parallel postulate to prove exterior angle theorem.

When you say that the sum of the angles in a triangle is 180°.

In elliptic geometry (https://en.wikipedia.org/wiki/Elliptic_geometry) the sum of the angles is >180° and in hyperbolic geometry (https://en.wikipedia.org/wiki/Hyperbolic_geometry) the sum of the angles is <180°.

 

[parshyaa]

When you say that the sum of the angles in a triangle is 180°.

So what do u want to say?
Let just stick to the euclidian geometry,
Then in euclidian geometry we can prove sum of angles of a triangle equals 180°
Because total angle of a straight line equals 180°.
What is wrong in my proof
So what do you want to justify, can't we prove total angle in a triangle equals 180° in euclidian geometry.

 

[parshyaa]

When you say that the sum of the angles in a triangle is 180°.

In elliptic geometry (https://en.wikipedia.org/wiki/Elliptic_geometry) the sum of the angles is >180° and in hyperbolic geometry (https://en.wikipedia.org/wiki/Hyperbolic_geometry) the sum of the angles is <180°.

I think you are right
Because in proving parallel postulate i used angle sum property of triangle and in proving triamgle sum property i have to use parallel postulate and thus its absured

 

[phyzguy]

When you say "Let's just stick to Euclidean Geometry", this is equivalent to assuming the Parallel Postulate. Euclid assumed the Parallel Postulate to be true. That's why it's called "Euclidean Geometry"

 

[a-nobody]

Please note that in small scales Euclid's parallel postulate is always true.
It's only when great distances come into play that it's not true.
Otherwise we couldn't do maths and physics!

 

[parshyaa]

Please note that in small scales Euclid's parallel postulate is always true.
It's only when great distances come into play that it's not true.
Otherwise we couldn't do maths and physics!

What does small scale means to you
Does it changes in a plane for larger distances?
or it changes when distances are measured on earth(because Earth is spherical and value changes).

 

[jbriggs444]

Please note that in small scales Euclid's parallel postulate is always true.

That depends on how you phrase the parallel postulate.

"Given a line and a point not on that line there is exactly one line parallel to the given line containing the given point"?

Always false on small scales.

 

[a-nobody]

Yes, always true. Why not? It gives rise to the Pythagorean Theorem always true and measurable and verifiable locally, in small everyday scales.

 

[jbriggs444]

Yes, always true. Why not? It gives rise to the Pythagorean Theorem always true and measurable and verifiable locally, in small everyday scales.

In mathematics, "true" and "approximately true" are not synonymous.

 

[a-nobody]

In mathematics, "true" and "approximately true" are not synonymous.

In the context of what you said:

"Given a line and a point not on that line there is exactly one line parallel to the given line containing the given point"?

"Always false on small scales."

I've never encountered the Pythagorean Theorem to be true in the neighborhood of a point and false or approximately true in another.

 

[jbriggs444]

In the context of what you said:

"Given a line and a point not on that line there is exactly one line parallel to the given line containing the given point"?

"Always false on small scales."

I've never encountered the Pythagorean Theorem to be true in the neighborhood of a point and false or approximately true in another.

Two lines (in a plane) are "parallel" if they contain no points in common. Given a line and a point not on that line, there are many lines that are "parallel" to the given line and that contain the given point as long as we consider only the local area.

That has nothing to do with the Pythagorean theorem.

Now let us proceed to your claim that the Pythagorean theorem is true and verifiable as long as we restrict our attention to a local area. Consider, for example, a spherical geometry. For any non-degenerate triangle in the geometry, no matter how small, the Pythagorean theorem will always be false. It will never be verifiable by physical measurement.

 

[a-nobody]

I respectfully disagree. Ever since Gauss and his magnificent "Disquisitiones generales circa superficies curvas" the area of the infinitesimal orthogonal triangle on the surface to find the curvature is taken to be: base x height / 2 completely on good terms with the Pythagorean Theorem.
I won't even mention that every manifold is homeomorphic to Euclidean space near a point.
By every physical measurement then as long as we probe close enough in the vicinity of a point, the Pythagorean Theorem is true. I hope that we are all in agreement that if the Pythagorean Theorem is true then the space is Euclidean and that there is a unique line parallel from some point to a nearby neighboring line. If there is a pencil of parallel lines to it, this becomes visible only as we approach infinity and the space deviates from Euclidean, if at all.
I really do not understand what your argument is about.

 

[jbriggs444]

I respectfully disagree. Ever since Gauss and his magnificent "Disquisitiones generales circa superficies curvas" the area of the infinitesimal orthogonal triangle on the surface to find the curvature is taken to be: base x height / 2 completely on good terms with the Pythagorean Theorem.
I won't even mention that every manifold is homeomorphic to Euclidean space near a point.
By every physical measurement then as long as we probe close enough in the vicinity of a point, the Pythagorean Theorem is true. I hope that we are all in agreement that if the Pythagorean Theorem is true then the space is Euclidean and that there is a unique line parallel from some point to a nearby neighboring line. If there is a pencil of parallel lines to it, this becomes visible only as we approach infinity and the space deviates from Euclidean, if at all.
I really do not understand what your argument is about.

The Pythagorean Theorem is false in spherical geometries. You cannot make it true by using smaller triangles. You can only make it "almost true".

 

[fresh_42]

The external angle theorem, as you have stated it, is only provable if we assume the parallel postulate to be true. So your proposed proof of the parallel postulate is circular.

... answers the original question.

When you say "Let's just stick to Euclidean Geometry", this is equivalent to assuming the Parallel Postulate. Euclid assumed the Parallel Postulate to be true. That's why it's called "Euclid

... is the only valid definition here.

Two lines (in a plane) are "parallel" if they contain no points in common. Given a line and a point not on that line, there are many lines that are "parallel" to the given line and that contain the given point as long as we consider only the local area.

That has nothing to do with the Pythagorean theorem.

... is correct and nothing has to be added.

I respectfully disagree.

This is your personal right. Fortunately it doesn't change the truth value of what has been said.

Ever since Gauss and his magnificent "Disquisitiones generales circa superficies curvas" the area of the infinitesimal orthogonal triangle on the surface to find the curvature is taken to be: base x height / 2 completely on good terms with the Pythagorean Theorem.

... So? Yes, Gauß worked as a land surveyor. Yes, nobody stated anything else. Yes, this involved non Euclidean geometry. However, non Euclidean geometry is not subject to this thread. Also the term local is completely inappropriate in this context. It seems that you are talking about some kind of manifolds, in which case some of your assertions might make sense. Unfortunately we deal with a manifold here, which is not only locally Euclidean, but globally. Furthermore we are neither interested in the topology, which is quite boring in a metric Euclidean space, nor in the analysis on it. Our space is globally flat and isomorphic, homeomorphic, diffeomorphic or whatever you like to $\mathbb{R}^2$, because it is $\mathbb{R}^2$.

Since the OP's question has been answered and this debate started to create confusion rather than clearance, I close it.
In the case someone of the participants wants to start a discussion on non Euclidean geometries on Riemannian manifolds, please state all given facts at the beginning of a new thread. Here we have a simple Euclidean plane and classic geometry. No add-ons needed.